Клинбиз | Клининговая компания в Нижнем Новгороде | Цены на клининговые услуги и уборку

Расчет факторинга ✓ блог НФК

Банк НФК (АО) Контакты:

Адрес: ул. Кожевническая, д. 14 115114 Москва, Телефон:(495) 787-53-37, Телефон:(495) 995-21-31, Электронная почта: [email protected]

Адрес2: ул. Рокоссовского, д. 62, БЦ «ВолгоградСИТИ», оф. 15-21 400050 г. Волгоград, Телефон:(8442) 43-44-00, Электронная почта: [email protected]

Адрес3: ул.Свободы, д. 73, офис 311 394018 Россия, г. Воронеж, Телефон:(473) 228-19-78, 228-19-79, Электронная почта: sav_av@factoring.

ru

Адрес4: ул. Хохрякова, 10, оф. 504-505 620014 Свердловская область, г. Екатеринбург, Телефон:(343) 310-14-55, Электронная почта: [email protected]

Адрес5: ул. Рабочая, д. 2а, офис 29А (3952) 486 331 г. Иркутск, Телефон:(3952) 486 331, Электронная почта: [email protected]

Адрес6: ул. Декабристов, 85б, офис 409, 410 420034 г. Казань, Телефон:(843) 200-09-47, 200-10-35, Электронная почта: [email protected]

Адрес7: Ленинский пр. , д. 30, офис 508 236006 г. Калининград, Телефон:(4012) 53-53-87, Электронная почта: [email protected]

Адрес8: ул. Красная д. 152 г. Краснодар, Телефон:(861) 226-42-52, 226-45-54, Электронная почта: [email protected]

Адрес9: ул. Алексеева, д. 49, офис 6-14. 660077 г. Красноярск, Телефон:(391) 200-28-20, Электронная почта: [email protected]

Адрес10: ул. Нижегородская, 24 603000 г.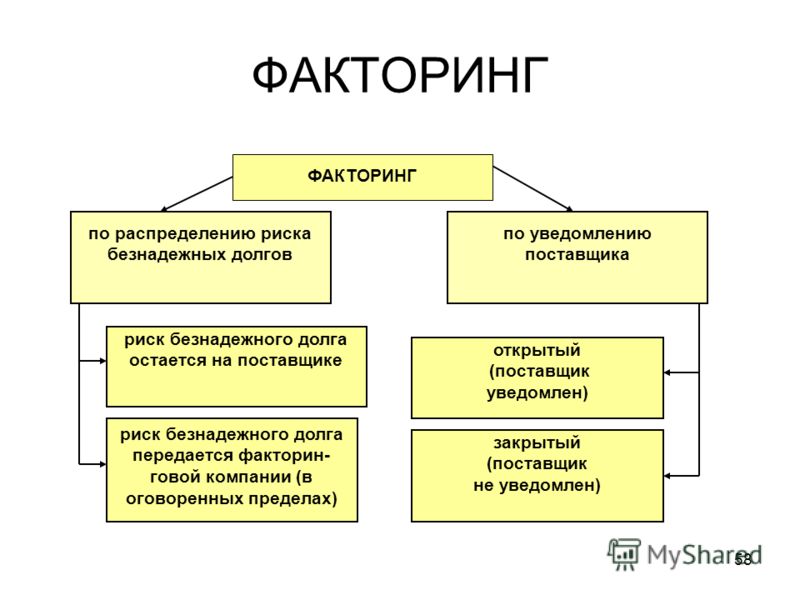 Нижний Новгород, Телефон:(831) 288-02-89, Электронная почта: [email protected]

Адрес11: ул. Ленина, 52, офис 505 630004 г. Новосибирск, Телефон:(383) 212-06-18, 212-06-19, Электронная почта: [email protected]

Адрес12: ул. Николая Островского, 59/1 614007 г. Пермь, Телефон:(342) 211-50-28, Электронная почта: [email protected]

Адрес13: ул. Красноармейская, д. 200, 8 этаж, оф. 803 344000 г. Ростов-на-Дону, Телефон:(863) 263-88-30, Электронная почта: kac_ay@factoring.

ru

Адрес14: пр.К.Маркса, д.201 «Б» (бизнес-крепость «Башня») 443080 г. Самара, Телефон:(846)993-61-62, 993-61- 64, 993-61-63, Электронная почта: [email protected]

Адрес15: ул. Восстания, 18, офисы 405-407 191014 Санкт-Петербург, Телефон:(812) 644-40-71, Электронная почта: [email protected]

Адрес16: ул.Танкистов, д.37, оф.304, 305 410019 г. Саратов, Телефон:(8452) 57-27-63, Электронная почта: [email protected]

Адрес17: ул. Крупской, д. 9, офис 727, 728, 729 450000 Республика Башкортостан, г. Уфа, Телефон:(347) 273-50-78, Электронная почта: [email protected]

Адрес18: ул. К. Маркса, д.38, офис 319 454091 г. Челябинск, Телефон:(351) 239-93-90, 239-93-91, 239-93-92, Электронная почта: [email protected]

Адрес19: ул. Республиканская, д.3, корпус 1, офис 404 150003 г. Ярославль, Телефон:(4852) 58-11-88, Электронная почта: [email protected]

Стороны факторинговой сделки — фактор, клиент, дебитор, все о сторонах факторинговой сделки

Чтобы эффективно использовать возможности факторинга, нужно хорошо понимать механизм взаимодействия участвующих в сделке компаний: клиента, его контрагента и фактора (финансирующей организации). О том, кто и как заключает факторинговую сделку, читайте в нашем материале. 

Три стороны факторинговой сделки

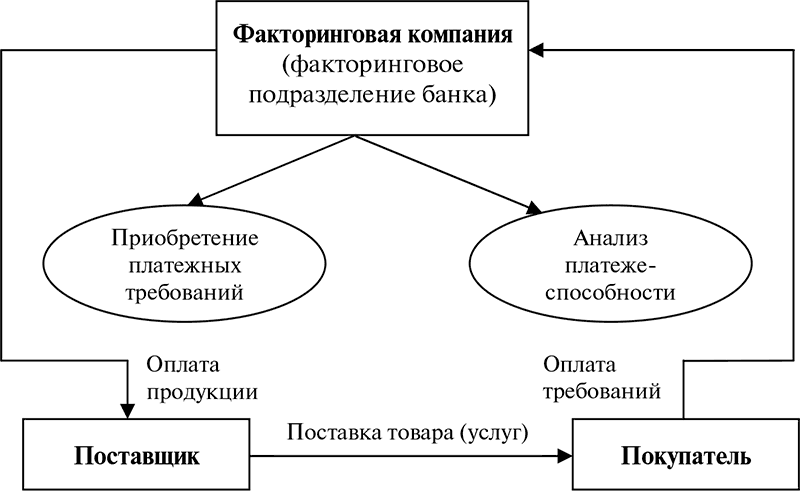
Факторинг – это вид финансирования, суть которого и структура сделки принципиально отличаются от более привычных кредитов и займов. Среди основных отличий то, что в факторинговой сделке участвуют не две, а три стороны – исполнитель контракта, его заказчик и факторинговая компания.

·        Поставщик или подрядчик (исполнитель контракта) – поставляет товар, оказывает услуги, выполняет работы по контракту с заказчиком.

·        Заказчик (покупатель) – согласно контракту с исполнителем обязан произвести оплату товара, работ или услуг денежными средствами.

·        Факторинговая компания (фактор) – выплачивает финансирование поставщику или подрядчику, погашая денежные обязательства заказчика.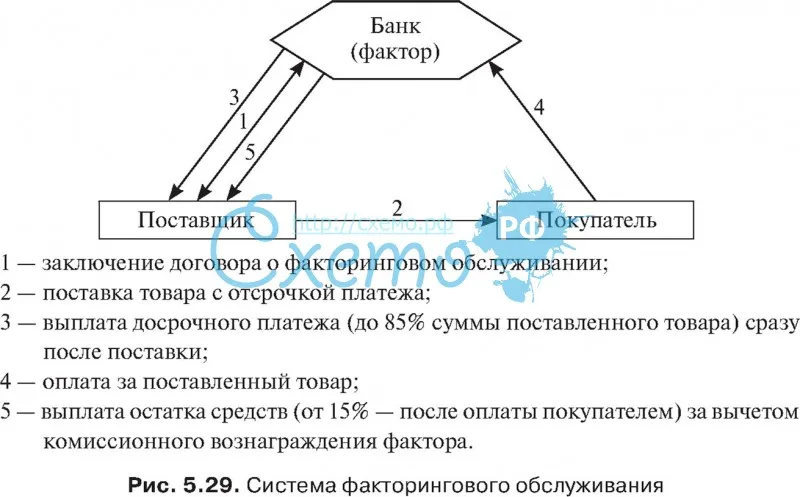 Взамен у фактора появляется право требовать от заказчика оплату обязательств, а в качестве вознаграждения за свои услуги компания получает факторинговую комиссию.

Таким образом, в стандартном контракте между заказчиком и исполнителем появляется третья сторона. Факторинговая компания вначале оплачивает вместо заказчика исполнителю товар, работы или услуги, а затем заказчик рассчитывается не с поставщиком или подрядчиком, а с оплатившей обязательства факторинговой компанией.

Подробнее о сути сделок под уступку денежных требований – в статье «Что такое факторинг?»

Заметим, что при оформлении факторинга права и обязанности сторон контракта не меняются – поставщик все так же обязан качественно исполнить контракт, а заказчик – оплатить его. Меняется только кредитор по уступленным денежным требованиям и (по согласованию сторон) срок оплаты этих обязательств – с помощью факторинга заказчик может увеличить отсрочку платежа.

Три роли в договоре факторинга

Испытывать потребность в факторинговом финансировании может как исполнитель контракта, так и его заказчик:

·        Поставщик или подрядчик с целью быстро пополнить оборотный капитал, закрыть кассовые разрывы привлекает досрочную оплату дебиторской задолженности заказчика.

·        Заказчик может быть инициатором факторинга, чтобы оплатить аванс поставщику, удлинить отсрочку платежа или иметь более удобный график погашения задолженности.

Именно та сторона, которая инициирует получение финансирования, и будет являться клиентом факторинговой компании. А значит, роли в договоре факторинга могут не совпадать с определением сторон факторинговой сделки:

·        Клиент (поставщик или заказчик, инициатор сделки) – подает заявку на финансирование, заключает договор факторинга и оплачивает комиссию.

·        Дебитор (контрагент клиента, вторая сторона финансируемого контракта) – согласует уступку денежного требования.

·        Фактор (факторинговая компания) – осуществляет финансирование.

Таким образом, если речь о классическом факторинге – когда поставщик уступает факторинговой компании денежные требования к заказчику по уже исполненному контракту – клиентом будет поставщик, а дебитором – заказчик. Если речь, например, о факторинге аванса (когда фактор вместо заказчика выплачивает поставщику предоплату по контракту) – то клиентом будет заказчик, а дебитором поставщик.

О том, как заключить договор и получить онлайн-финансирование, читайте в статье «Схема выдачи бездокументарного факторинга»

---

Заинтересовала услуга онлайн-факторинга? Чтобы узнать индивидуальные условия финансирования для вашей компании, подайте заявку в личном кабинете на GetFinance или свяжитесь со специалистом компании по телефону 8 (800) 500 55 52.

 

Договор факторинга. Образец заполнения и бланк 2021 года

Договор факторинга (или договор финансирования) подразумевает двухстороннее соглашение, в силу которого один участник договора (финансовый агент), передает своему контрактуальному партнеру (клиенту) деньги в обмен на право денежных требований к третьему лицу – должнику.

Файлы в .DOC:Бланк договора факторингаОбразец договора факторинга

Суть договора и правовое регламентирование

Правовое регулирование правоотношений факторинга осуществляется на основании статьи 824 ГК РФ. В соответствии со смыслом статьи, под договором факторинга подразумевается финансирование под уступку материального (денежного) требования.

Само финансирование при этом подразумевает возмездность услуги. Условиями договора, таким образом, становятся следующие действия контрагентов:

1. Финансовый агент передает своему контрагенту (клиенту) финансовые средства в виде займа или аванса.
2. Контрагент (клиент) уступает финансовому агенту имеющееся у него право требовать возврата денег у третьего лица (должника).

Обязанности и права финансового агента

К обязанностям и правам финансового агента как субъекта договора факторинга относятся следующие действия, которые ему надлежит выполнить в рамках договора:

• передать деньги клиенту в размере, соразмерном праву истребования долга с третьего лица;
• принять на себя обязанности по учету требований клиента к должникам;
• предпринять меры по обеспечению возврата должниками денежных средств;
• воплотить свое право требования, то есть предъявить должникам претензии по выплатам долга;
• принять от должников платежи.

Также договор может предусматривать обязанность финансового агента вести бухгалтерский учет в интересах клиента и предоставлять ему другие услуги по предмету договора, то есть по долговым обязательствам должников.

Выступать в качестве финансового агента может любое кредитное учреждение, в частности, при попытке клиента получить кредит в банке.

Если банк усомнится в платежеспособности клиента, но положительно оценит имеющиеся у клиента права по истребованию долгов, то кредит может быть выдан на основании договора факторинга, причем долговые обязательства клиент предоставит банку в качестве залога или гарантий.

Если клиент сможет закрыть кредит, то права требования долгов вернутся к нему, если же нет, то эти права перейдут в собственность кредитора.

Предмет договора факторинга

Услуга, оказываемая финансовым агентом своему клиенту, является тем стержнем, на котором основываются все условия договора факторинга. Причем оказываемая услуга является разноплановой и включает в себя несколько форм гражданско-правовых отношений, к примеру:

• уступку права требования;
• заем или кредитования;
• аванс;
• оказание услуг и т.д.

Легче будет рассмотреть договор факторинга на небольшом примере.

Прикладной факторинг

В качестве субъекта примера будет удобно взять некую крупную компанию «А», среди заказчиков которой имеется большое количество должников.

Несмотря на обширный фронт работ и заказов, у компании «А» начинаются финансовые проблемы, связанные с задержкой оплаты ее товаров или услуг.

Помочь такой компании сможет организация «Б», специализирующаяся на истребовании долгов за вознаграждение. Она переведет на счет компании денежные средства, в которых та нуждается, а взамен получит от нее право истребовать долг с должников.

Оформляться эта помощь будет в виде договора факторинга, по условиям которого «А» получит деньги для продолжения своей деятельности, а «Б» – должника, от которого будет требовать возврата долга.

Содержание договора и особые услуги

В тексте договора контрагенты оговаривают:

1. вид факторинга;
2. объем денежных средств, получаемый клиентом от финансового агента;
3. объем комиссионного вознаграждения финансового агента;
4. гарантии, предоставляемые контрагентами друг другу;
5. ответственность за неисполнение условий договора;
6. другие условия, которые стороны пожелают закрепить в договоре.

К другим (дополнительным) услугам, устанавливаемым на усмотрение сторон договора факторинга, может относиться осуществление бухгалтерских операций по учету долговых требований.

Подобная услуга будет актуальной в случае, если клиент передает финансовому агенту право требования по долговым обязательствам в отношении многих или нескольких должников.

Виды факторинга

Под видом договора факторинга подразумевается способ уступки денежных требований. Так, клиент по договору может:

• обменять право денежных требований на денежное финансирование со стороны финансового агента;
• передать право денежных требований финансовому агенту в виде залога, призванного обеспечить возврат финансирования. Право требования в таком случае перейдет к финансовому агенту только в случае, если клиент не сможет вернуть сумму, полученную от финансового агента в порядке финансирования по договору факторинга.

Другое разделение по видам факторинга осуществляется в силу реальности либо консенсуальности договорных обязательств.

В зависимости от подобного деления можно говорить о потенциальной возможности либо невозможности принудить финансового агента к выдаче кредита клиенту, а клиента принудить к передаче права требования долговых обязательств.

Если договор факторинга является консенсуальным, то права и обязанности контрагентов возникнут после достижения ими соглашения по условия договора. При реальном характере договора права и обязанности возникнут только при передаче предмета договора, то есть денег и долговых обязательств.

Консенсуальный договор даст сторонам право принудить своего контрагента к передаче предмета договора. При реальном характере договора такого права у контрагентов не будет.

Часть 1 статьи 824 ГК позволяет сторонам заключение договора с осуществлением передачи предмета договора как в реальном времени, так и в будущем.

Риски факторинга

Как и любые кредитные правоотношения, договор факторинга относится к типу договоров с повышенными рисками.

Поэтому до момента заключения договора финансовому агенту требуется проведение тщательного анализа финансового положения контрагента и должника (должников) с тем, чтобы убедиться в возможности возврата затраченных кредитных средств.

Анализ производится по нескольким позициям:

• ликвидность баланса;
• срок задолженности;
• состав задолженности;
• конкурентоспособность и возможность реализации выпускаемой клиентом или должником продукции;
• рынок, на котором сбывается продукция клиента или должника;
• конъюнктура рынка сбыта;
• платежеспособность клиента и должника и т.д.

Проведение анализа осуществляется аналитиками финансового агента на основании:

• бухгалтерской документации клиента или должника;
• кредитных историй клиента или должника;
• информация в средствах массовой информации, касающаяся клиента или должника и т.д.

При наличии заявки клиента на кредит на условиях договора факторинга кредитная организация обязана осуществить анализ в течение двух недель.

При положительных выводах по результатам проведения анализа кредитная организация (банк) заключает с клиентом договор факторинга с обязательным включением в текст договора следующих позиций:

• верхний лимит кредитной суммы, выдаваемой клиенту;
• верхний лимит долговых обязательств, принимаемых на инкассо.

Лимит кредитной суммы определяется исходя из объема долговых обязательств, право на которые имеет клиент по договору факторинга.

Сроки

Закон не регламентирует срок, на который может быть заключен договор факторинга, то есть длительность договора всецело оставляется на усмотрение контрагентов. Практика показывает, что минимальный срок действия договора факторинга не может быть менее одного года.

Факторинг

Пример факторинга существующих денежных требований

Один из наиболее распространенных видов факторинга – досрочная оплата исполненных контрактов (этапов контракта), по которым предусмотрена отсрочка платежа. Пример: поставщик заключил контракт на поставку текстильной продукции в течение года. При этом поставка осуществляется ежемесячно по заявкам заказчика, а оплата происходит в конце срока – 31 декабря. Таким образом, поставщик ежемесячно привозит товар и получает закрывающий документ на поставленный объем и сумму. Поставщик может уступить задолженность заказчика по закрывающему документу факторинговой компании и сразу же получить до 90% от суммы поставки. Выплата финансирования производится на расчетный счет поставщика в течение 24 часов с момента подписания сторонами реестра денежных требований.

В согласованный срок заказчик оплачивает свои обязательства по контракту, но не поставщику, а факторинговой компании, так как была оформлена уступка задолженности.

Пример факторинга аванса

Подрядчик заключил контракт на строительство больницы, при этом предусмотрена выплата аванса в размере 30% от цены контракта. У заказчика нет возможности оплатить аванс, из-за чего подрядчик не приступает к исполнению контракта. Заказчик может обратиться в факторинговую компанию и оформить факторинг аванса. Факторинговая компания выполняет обязательства заказчика и выплачивает подрядчику до 100% от суммы предусмотренного аванса, выплата средств производится на расчетный счет подрядчика в течение 24 часов с момента подписания сторонами реестра денежных требований. Подрядчик приступает к исполнению контракта. Заказчик в согласованный и удобный для него срок погашает задолженность перед факторинговой компанией, возвращая ей сумму финансирования.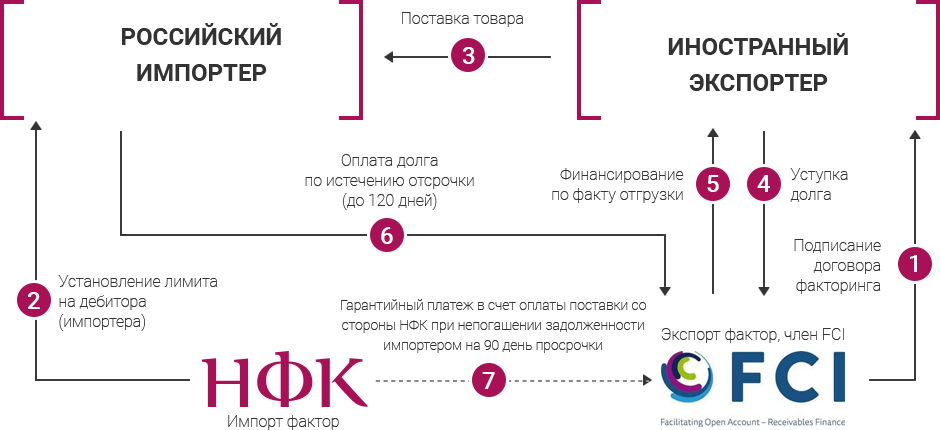

В факторинге аванса клиент (заказчик) уступает права будущего требования возврата аванса. Если поставщик не исполнит свои обязательства по контракту в срок, то он будет обязан вернуть выплаченный ему аванс. Но так как была оформлена уступка, то он вернет его не заказчику, а факторинговой компании, профинансировавшей контракт.

Пример факторинга качества

Поставщик заключил контракт на поставку нефтепродуктов в течение года. При этом поставка осуществляется ежемесячно по заявкам заказчика, а оплата происходит поквартально за весь объем продукции, отгруженной в течение 3 месяцев. Поставщик ежемесячно, с января по март, поставлял нефтепродукты, но 1 апреля заказчик не смог оплатить свои обязательства. Поставщик приостановил исполнение контракта до получения просроченной задолженности.

Чтобы расплатиться с поставщиком и возобновить поставки, заказчик обращается в факторинговую компанию и заключает договор факторинга качества. Факторинговая компания оплачивает обязательства заказчика перед поставщиком. Выплата средств производится на расчетный счет поставщика в течение 24 часов с момента подписания сторонами реестра денежных требований. В согласованный и удобный для него срок заказчик погашает задолженность факторинговой компании.

В факторинге качества клиент (заказчик) уступает права будущего требования возврата денежных средств, которые могут возникнуть из-за претензий к качеству товара. Если поставщик поставит некачественный товар, то он обязан вернуть полученные по контракту средства. Но так как была оформлена уступка, то он вернет их не заказчику, а факторинговой компании, профинансировавшей контракт.

Пример интеграции ЭДО в банке «Кольцо Урала» — Диадок

Задача

Сократить срок доставки документов, подтверждающих факт поставки

Факторинговой компании для оказания услуг финансирования требуются документы, подтверждающие факт поставки (выполнения работ или оказания услуг). При бумажном документообороте процесс обмена документами занимает до нескольких дней, в зависимости от удаленности клиента. В условиях рыночной конкуренции преимуществом Фактора является высокая скорость принятия решений и выдачи финансирования. Обмен скан-копиями документов через электронную почту не решает данную проблему, так как они не имеют юридической значимости.

Решение

Для упрощения документооборота с Клиентами, делая ставку на современные технологии ведения бизнеса, Факторинговая компания «КОЛЬЦО УРАЛА», подключилась к системе электронного документооборота Контур. Диадок оператора СКБ Контур. Определяющими условиями при выборе оператора стали:

• успешный опыт внедрения системы в факторинговых компаниях;
• получение бесплатной помощи службы технической поддержки круглосуточно;
• возможность бессрочного бесплатного хранения информации на серверах оператора даже после окончания договорных отношений.

Сотрудники Факторинговой компании «КОЛЬЦО УРАЛА» быстро освоили работу через веб-интерфейс Контур. Диадок, а наличие функционала согласования и распределения документов по подразделениям позволило организовать внутреннюю работу с электронными документами.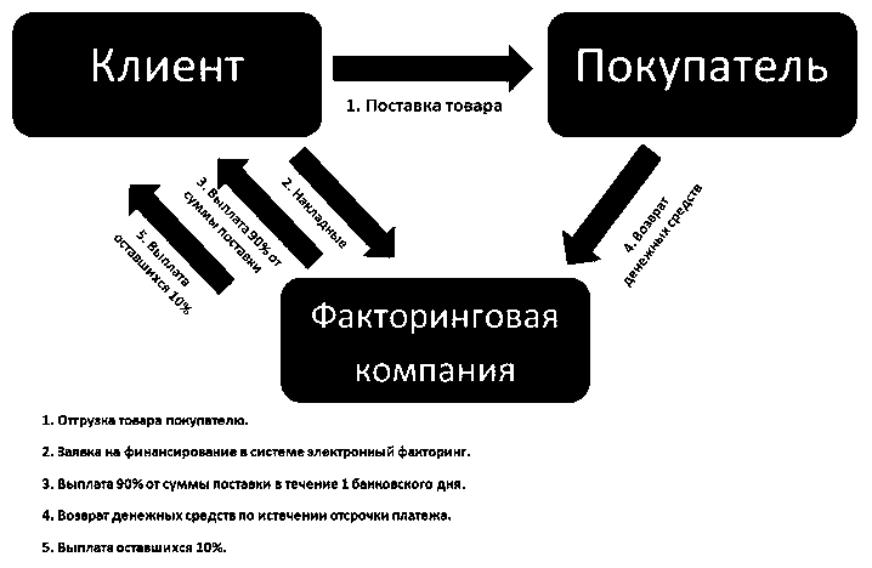

Затем Компания начала работу по привлечению своих клиентов к обмену электронными документами, при этом, все расходы по подключению контрагентов Факторинговая компания «КОЛЬЦО УРАЛА» взяла на себя, поэтому для клиентов использование Контур.Диадока стало не только удобным, но и бесплатным. Благодаря этому повысились клиентская лояльность и конкурентоспособность компании.

Результаты

Сегодня клиентская база компании составляет сотни контрагентов, и большинство из них работают через Контур. Диадок. Ежемесячно Факторинговая компания «КОЛЬЦО УРАЛА» получает более 1 000 электронных документов.

У клиентов компании появилась возможность отказаться от физической доставки документов для получения сумм финансирования. Направление через систему ЭДО и подписание электронной подписью обеспечивает юридическую силу и мгновенную доставку таких документов, а выплата финансирования происходит в течение двух часов.

Кроме того, Факторинговая компания «КОЛЬЦО УРАЛА». через Контур.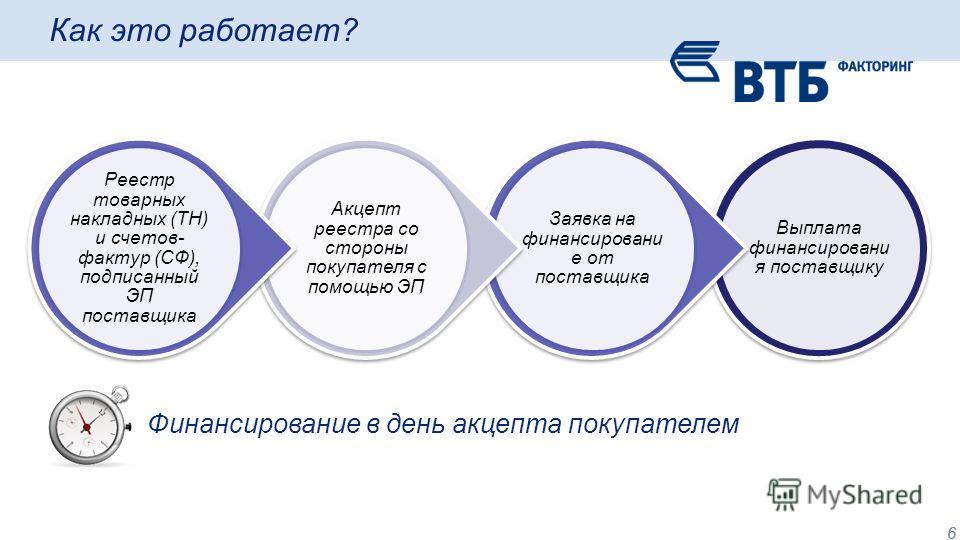 Диадок передает своим клиентам акты об оказании услуг, счета-фактуры, счета на оплату и другие документы, связанные с исполнением договоров.

Комментарии

Юлия Иващенко
Заместитель директора по операционной деятельности ФК «КОЛЬЦО УРАЛА»

Сегодня не все наши клиенты готовы к обмену электронными документами: для некоторых это нечто совсем новое, есть опасения, страх неизвестности. Однако, мы уверены, что со временем все они освоят эту современную технологию и перейдут на электронное взаимодействие. Сегодня у нас нет никаких препятствий для того, чтобы оперативно перевести деньги со своего счета на счет клиента. Благодаря ЭДО мы значительно расширили географию оказания услуг, потому что теперь мы можем оперативно работать с клиентами далеко за пределами Свердловской области

Павел Коптелов
Руководитель отраслевого направления СКБ Контур

Клиенты факторинговых компаний уже видят преимущества, которые дает внедрение электронного документооборота — чем быстрее подписанный сторонами ТОРГ-12 попадает к фактору, тем быстрее, Поставщик получит финансирование. В этом заинтересованы все три стороны процесса. – С помощью Диадока передача документа от одного звена до другого происходит моментально, тогда как при бумажном документообороте это занимало больше недели. Таким образом, те клиенты, которые обмениваются с компанией Кольцо Урала юридически значимыми документами в электронном виде, могут получить финансирование всего за пару часов.

Пример факторинга

В большинстве, факторингом пользуются небольшие компании, т.е. компании, которые не имеют возможности получить кредитное финансирование от Банков.

Рассмотрим порядок действий на примере факторинга, при котором осуществляется финансирование от факторинговой фирмы.

• 1. Поставщик обращается в факторинговую фирму за предоставлением финансирования по предстоящей отгрузке и предоставляет факторинговой компании все необходимые документы:
  • a. Юридические и уставные документы,
  • b. бухгалтерские отчеты, включающие в себя несколько периодов,
  • c. заполненная Анкета на свою компанию,
  • d. заполненная Анкета на покупателя, которого поставщик хочет передать на факторинг,
  • e. копия договора поставки с данным покупателем.
• 2. По договору с отсрочкой платежа сроком от 30 до 120 дней, поставщик отгружает покупателю продукцию.
• 3. Покупатель фиксирует факт получения товара и фиксирует это в отгрузочных документах поставщика.
• 4. Поставщик после отгрузки письмом уведомляет покупателя о том, что оплата за отгруженную продукцию должна быть переведены на расчетный счет факторинговой компании.
• 5. Факторинговая компания, на основании факта передачи поставщика покупателю письма, выдает поставщику денежные средства в сумме до 90% от объема поставленного покупателю товара.
• 6. По окончании отсрочки платежа, то есть срока от 30 до 120 дней, покупатель перечисляет сумму своей кредиторской задолженности не поставщику, а факторинговой фирме.
• 7. По факту оплаты задолженности от покупателя, факторинговая фирма начисляет комиссию поставщику.
• 8. Поставщик оплачивает факторинговой компании комиссию за предоставленное финансирование.
• 9. Факторинговая фирма, в случае возникновения разницы, перечисляет ее поставщику. Разница состоит из:
  • a. СУММА за отгруженный товар покупателя, МИНУС
  • b. СУММА, выплаченного финансирования поставщику, и МИНУС
  • c. СУММА комиссии, оплаченная поставщиком факторинговой компании.

Комиссия начисляется от суммы предоставленного финансирования и зависит от:

• формы передачи дебиторской задолженности;
• срока отсроченного платежа.

В описанной схеме используется один из примеров факторинга, когда поставщик уверен в платежеспособности покупателя.

Какие же формы передачи дебиторской задолженности существуют?

Есть две формы:

Регрессивная

Поставщик уверен в том, что покупатель оплатит товар и обязуется в случае неуплаты вернуть факторинговой компании полученное финансирование. Срок отсроченного платежа здесь может быть 30-45 дней.

Без регресса

Поставщик не уверен в платежеспособности покупателя и передает факторинговой фирме дебиторскую задолженность покупателя.

В случае неуплаты покупателем задолженности, факторинговая фирма сама предпринимает действия по возврату задолженности от покупателя.

Срок предоставленного финансирования в этом случае составляет 30-120 дней. Размер комиссии при этой форме финансирования значительно больше.

Комиссия состоит из следующих частей, и облагается НДС:

• Комиссия за финансирование, которая начисляется в процентах годовых;
• Комиссия за обслуживание в факторинговой фирме, которая начисляется в процентах от объема отгруженной продукции;
• Сбор за обработку документов.

Читайте также

Видеоинструкции по работе — Электронный факторинг — СКБ Контур

Заполните, пожалуйста, все поля.

Кому:

Электронный факторинг   

Ваше имя: *

Электронная почта: *

Телефон:

Название организации:

ИНН:

Регион: *

01 – Республика Адыгея02 – Республика Башкортостан03 – Республика Бурятия04 – Республика Алтай05 – Республика Дагестан06 – Республика Ингушетия07 – Республика Кабардино-Балкария08 – Республика Калмыкия09 – Республика Карачаево-Черкесия10 – Республика Карелия11 – Республика Коми12 – Республика Марий Эл13 – Республика Мордовия14 – Республика Саха (Якутия)15 – Республика Северная Осетия — Алания16 – Республика Татарстан17 – Республика Тыва18 – Республика Удмуртия19 – Республика Хакасия20 – Республика Чечня21 – Республика Чувашия22 – Алтайский край23 – Краснодарский край24 – Красноярский край25 – Приморский край26 – Ставропольский край27 – Хабаровский край28 – Амурская область29 – Архангельская область30 – Астраханская область31 – Белгородская область32 – Брянская область33 – Владимирская область34 – Волгоградская область35 – Вологодская область36 – Воронежская область37 – Ивановская область38 – Иркутская область39 – Калининградская область40 – Калужская область41 – Камчатский край42 – Кемеровская область43 – Кировская область44 – Костромская область45 – Курганская область46 – Курская область47 – Ленинградская область48 – Липецкая область49 – Магаданская область50 – Московская область51 – Мурманская область52 – Нижегородская область53 – Новгородская область54 – Новосибирская область55 – Омская область56 – Оренбургская область57 – Орловская область58 – Пензенская область59 – Пермский край60 – Псковская область61 – Ростовская область62 – Рязанская область63 – Самарская область64 – Саратовская область65 – Сахалинская область66 – Свердловская область67 – Смоленская область68 – Тамбовская область69 – Тверская область70 – Томская область71 – Тульская область72 – Тюменская область73 – Ульяновская область74 – Челябинская область75 – Забайкальский край76 – Ярославская область77 – Москва78 – Санкт-Петербург79 – Еврейская АО83 – Ненецкий АО86 – Ханты-Мансийский АО87 – Чукотский АО89 – Ямало-Ненецкий АО91 – Республика Крым92 – Севастополь99 – Байконур

Вопрос: *

Факторинговая квадратичность

«Факторинг» (или «Факторинг» в Великобритании) Квадратичный равен:

найти, что умножить, чтобы получить квадратичный

Это называется «факторинг», потому что мы находим коэффициенты (коэффициент — это то, на что мы умножаем)

Пример:

Умножение (x + 4) и (x − 1) вместе (так называемое расширение) дает x ² + 3x — 4 :

Таким образом, (x + 4) и (x − 1) являются множителями x ² + 3x — 4

На всякий случай проверим:

(х + 4) (x − 1) = x (x − 1) + 4 (x − 1)

= х ² — х + 4х — 4

= х ² + 3х — 4

Да, (x + 4) и (x − 1) определенно являются множителями x ² + 3x — 4

Вы видели, что расширение и факторинг — противоположности?

Расширение обычно легко, но факторинг часто бывает сложным .

Это все равно, что пытаться найти, какие ингредиенты
пошли на торт, чтобы сделать его таким вкусным.
Это сложно понять!

Итак, давайте попробуем пример, где мы еще не знаем факторов:

Общий коэффициент

Сначала проверьте, есть ли общие факторы.

Пример: каковы множители 6x

² — 2x = 0?

6 и 2 имеют общий множитель 2 :

2 (3x ² — x) = 0

И x ² и x имеют общий множитель x :

2x (3x — 1) = 0

И мы это сделали! Коэффициенты: 2x и 3x — 1 ,

.

Теперь мы также можем найти корни (где он равен нулю):

• 2x равно 0, когда x = 0
• 3x — 1 равно нулю, когда x = 1 3

А это график (посмотрите, как он равен нулю при x = 0 и x = 1 3 ):

Но это не всегда так просто. ..

Угадай и проверь

Может, ответ дадим?

Пример: каковы множители 2x

² + 7x + 3?

Нет общих факторов.

Давайте попробуем угадать ответ, а затем проверим, правы ли мы … нам может повезти!

Мы могли угадать (2x + 3) (x + 1):

(2x + 3) (x + 1) = 2x ² + 2x + 3x + 3
= 2x ² + 5x + 3 (НЕПРАВИЛЬНО)

Как насчет (2x + 7) (x − 1):

(2x + 7) (x − 1) = 2x ² — 2x + 7x — 7
= 2x ² + 5x — 7 (СНОВА НЕПРАВИЛЬНО)

Хорошо, как насчет (2x + 9) (x − 1):

(2x + 9) (x − 1) = 2x ² — 2x + 9x — 9
= 2x ² + 7x — 9 (СНОВА НЕПРАВИЛЬНО)

О нет! Мы можем долго гадать, прежде чем нам повезет.

Это не очень хороший метод. Так что давайте попробуем что-нибудь еще.

Метод для простых случаев

К счастью, есть метод, который работает в простых случаях.

С квадратным уравнением в этой форме:

Шаг 1 : Найдите два числа, которые умножаются, чтобы получить ac (другими словами, a на c), и сложить, чтобы получить b.

Пример: 2x ² + 7x + 3

ac равно 2 × 3 = 6 , а b равно 7

Итак, мы хотим, чтобы два числа, которые умножались вместе, давали 6 и в сумме давали 7

Фактически это делают 6 и 1 (6 × 1 = 6 и 6 + 1 = 7)

Как найти 6 и 1?

Это помогает составить список факторов ac = 6 , а затем попытаться добавить некоторые, чтобы получить b = 7 .

Факторы 6 включают 1, 2, 3 и 6.

Ага! 1 и 6 складываются с 7 и 6 × 1 = 6.

Шаг 2 : Перепишите середину с этими числами:

Перепишите 7x с 6 x и 1 x:

2x ² + 6x + x + 3

Шаг 3 : Разложите на множители первые два и последние два термина по отдельности:

Первые два члена 2x ² + 6x разложить на 2x (x + 3)

Последние два члена x + 3 в данном случае фактически не меняются

Получаем:

2х (х + 3) + (х + 3)

Шаг 4 : Если мы сделали это правильно, два наших новых члена должны иметь четко видимый общий множитель.

В этом случае мы видим, что (x + 3) является общим для обоих терминов, поэтому мы можем пойти:

Начать с: 2x (x + 3) + (x + 3)

Что составляет: 2x (x + 3) + 1 (x + 3)

И так: (2x + 1) (x + 3)

Готово!

Проверить: (2x + 1) (x + 3) = 2x ² + 6x + x + 3 = 2x ² + 7x + 3 (Да)

Намного лучше, чем гадать!

Давайте снова посмотрим шаги с 1 по 4 за один раз :

2x 2 + 7x + 3

2x 2 + 6x + x + 3

2x (x + 3) + (x + 3)

2x (x + 3) + 1 (x + 3)

(2x + 1) (x + 3)

Хорошо, давайте попробуем другой пример:

Пример: 6x

² + 5x — 6

Шаг 1 : ac равно 6 × (−6) = −36 , а b равно 5

Перечислите положительные множители ac = −36 : 1, 2, 3, 4, 6, 9, 12, 18, 36

Одно из чисел должно быть отрицательным, чтобы получилось −36, поэтому, играя с несколькими разными числами, я обнаружил, что −4 и 9 работают хорошо:

−4 × 9 = −36 и −4 + ​​9 = 5

Шаг 2 : перепишите 5x с −4x и 9x:

6x ² — 4x + 9x — 6

Шаг 3 : Разложите на множители первые два и последние два:

2x (3x — 2) + 3 (3x — 2)

Шаг 4 : Общий множитель (3x — 2):

(2x + 3) (3x — 2)

Проверить: (2x + 3) (3x — 2) = 6x ² — 4x + 9x — 6 = 6x ² + 5x — 6 (Да)

В поисках чисел

Самая трудная часть — найти два числа, которые умножаются, чтобы получить ac, и складывать, чтобы получить b.

Это отчасти предположение, и помогает перечислить все факторы .

Вот еще один пример, который может вам помочь:

Пример: ac = −120 и b = 7

Какие два числа умножают на -120, и добавляют к 7 ?

Множитель 120 (плюс и минус):

1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60 и 120

Мы можем попробовать пары множителей (начнем с середины!) И посмотреть, прибавят ли они к 7:

• −10 x 12 = −120 и −10 + 12 = 2 (нет)
• −8 x 15 = −120 и −8 + 15 = 7 (ДА!)

Попрактикуйтесь

Почему фактор?

Что ж, одно из больших преимуществ факторизации состоит в том, что мы можем найти корней квадратного уравнения (где уравнение равно нулю).

Все, что нам нужно сделать (после факторинга), это найти, где каждый из двух множителей становится равным нулю

Пример: каковы корни (нули) у 6x

² + 5x — 6?

Мы уже знаем (сверху) коэффициенты

(2x + 3) (3x — 2)

И мы можем выяснить, что

(2x + 3) равно нулю, когда x = −3/2

и

(3x — 2) равно нулю, когда x = 2/3

Итак, корни 6x ² + 5x — 6 равны:

−3/2 и 2/3

Вот график 6x ² + 5x — 6, видите, где он равен нулю?

И мы также можем проверить это с помощью небольшой арифметики:

При x = -3/2: 6 (-3/2) ² + 5 (-3/2) — 6 = 6 × (9/4) — 15/2 — 6 = 54/4 — 15 / 2-6 = 6-6 = 0

При x = 2/3: 6 (2/3) ² + 5 (2/3) — 6 = 6 × (4/9) + 10/3 — 6 = 24/9 + 10/3 — 6 = 6-6 = 0

Графики

Мы также можем попробовать построить квадратное уравнение. Увидев, где он равен нулю, мы можем понять.

Пример: (продолжение)

Начиная с 6x ² + 5x — 6 и только этот участок:

Корни равны около x = −1,5 и x = +0,67, поэтому мы можем предположить , что корни равны:

−3/2 и 2/3

Что может помочь нам определить факторы 2x + 3 и 3x — 2

Всегда проверяйте! На графике значение +0.67 на самом деле может быть не 2/3

Общее решение

Существует также общее решение (полезно, когда описанный выше метод не срабатывает), в котором используется формула корней квадратного уравнения:

Используйте эту формулу, чтобы получить два ответа x ₊ и x _— (один для случая «+», а другой для случая «-» в «±»), и мы получим это факторинг :

а (х — х ₊ ) (х — х _— )

Давайте воспользуемся предыдущим примером, чтобы увидеть, как это работает:

Пример: каковы корни у 6x

² + 5x — 6?

Подставляем a = 6, b = 5 и c = −6 в формулу:

x = −b ± √ (b ² — 4ac) 2a

= −5 ± √ (5 ² — 4 × 6 × (−6)) 2 × 6

= −5 ± √ (25 + 144) 12

= −5 ± √169 12

= −5 ± 13 12

Итак, два корня:

х ₊ = (-5 + 13) / 12 = 8/12 = 2/3,

x _— = (−5 — 13) / 12 = −18/12 = −3/2

(Обратите внимание, что мы получаем тот же ответ, что и при факторинге ранее. )

Теперь поместите эти значения в (x — x ₊ ) (x — x _— ):

6 (х — 2/3) (х + 3/2)

Мы можем немного изменить это, чтобы упростить:

3 (х — 2/3) × 2 (х + 3/2) = (3x — 2) (2x + 3)

И мы получаем те же факторы, что и раньше.

362, 1203, 2262, 363, 1204, 2263, 2100, 2101, 2102, 2103, 2264, 2265

(Спасибо «mathsyperson» за части этой статьи)

Факторинговые квадратные уравнения — методы и примеры

Есть ли у вас представление о факторизации многочленов ? Поскольку теперь у вас есть основная информация о многочленах, мы узнаем, как решать квадратичные многочлены с помощью факторизации.

Прежде всего, давайте быстренько рассмотрим квадратное уравнение . Квадратное уравнение — это многочлен второй степени, обычно в форме f (x) = ax ² + bx + c, где a, b, c, ∈ R, и a ≠ 0. Термин «a» означает называется старшим коэффициентом, а «c» — абсолютным членом f (x).

Каждое квадратное уравнение имеет два значения неизвестной переменной, обычно называемых корнями уравнения (α, β). Мы можем получить корни квадратного уравнения, разложив уравнение на множители.

По этой причине факторизация является фундаментальным шагом на пути к решению любого уравнения в математике. Давайте разберемся.

Как разложить квадратное уравнение на множители?

Факторинг квадратного уравнения можно определить как процесс разбиения уравнения на произведение его факторов. Другими словами, мы также можем сказать, что факторизация — это обратное умножению.

Чтобы решить квадратное уравнение ax ² + bx + c = 0 путем факторизации, используются следующие шаги :

• Разверните выражение и при необходимости очистите все дроби.
• Переместите все члены в левую часть знака равенства.
• Факторизуйте уравнение, разбив средний член.
• Приравняйте каждый коэффициент к нулю и решите линейные уравнения

Пример 1

Решите: 2 (x ² + 1) = 5x

Решение

Разверните уравнение и переместите все члены слева от знака равенства.

⟹ 2x ² — 5x + 2 = 0

⟹ 2x ² — 4x — x + 2 = 0

⟹ 2x (x — 2) — 1 (x — 2) = 0

⟹ ( x — 2) (2x — 1) = 0

Приравняем каждый множитель к нулю и решим

⟹ x — 2 = 0 или 2x — 1 = 0

⟹ x = 2 или x = 1212

Следовательно, решения x = 2, 1/2.

Пример 2

Решить 3x ² — 8x — 3 = 0

Решение

3x ² — 9x + x — 3 = 0

⟹ 3x (x — 3) + 1 (x — 3) = 0

⟹ (x — 3) (3x + 1) = 0

⟹ x = 3 or x = -13

Пример 3

Решите следующее квадратное уравнение ( 2x — 3) ² = 25

Решение

Разверните уравнение (2x — 3) ² = 25, чтобы получить;

⟹ 4x ² — 12x + 9-25 = 0

⟹ 4x ² — 12x — 16 = 0

Разделите каждый член на 4, чтобы получить;

⟹ x ² — 3x — 4 = 0

⟹ (x — 4) (x + 1) = 0

⟹ x = 4 или x = -1

Существует множество методов факторизации квадратных уравнений. В этой статье мы сделаем акцент на том, как разложить квадратные уравнения на множители, в которых коэффициент при x ² равен 1 или больше 1.

Таким образом, мы будем использовать метод проб и ошибок, чтобы получить правильные множители. для данного квадратного уравнения.

Факторинг, когда коэффициент x

² равен 1

Чтобы разложить квадратное уравнение вида x ² + bx + c, старший коэффициент равен 1. Вам необходимо определить два числа, произведение и сумма которых равны c и b соответственно.

СЛУЧАЙ 1: Когда b и c положительны

Пример 4

Решите квадратное уравнение: x ² + 7x + 10 = 0

Перечислите множители 10:

1 × 10, 2 × 5

Определите два множителя с произведением 10 и суммой 7:

1 + 10 ≠ 7
2 + 5 = 7.

Проверьте множители, используя распределительное свойство умножения.

(x + 2) (x + 5) = x ² + 5x + 2x + 10 = x ² + 7x + 10

Факторы квадратного уравнения: (x + 2) (x + 5)

Приравнивание каждого множителя к нулю дает;

x + 2 = 0 ⟹x = -2

x + 5 = 0 ⟹ x = -5

Следовательно, решение x = — 2, x = — 5

Пример 5

х ² + 10х + 25.

Решение

Определите два фактора с произведением 25 и суммой 10.

5 × 5 = 25 и 5 + 5 = 10

Проверьте факторы.

x ² + 10x + 25 = x ² + 5x + 5x + 25

= x (x + 5) + 5x + 25

= x (x + 5) + 5 (x + 5)

= (x + 5) (x + 5)

Следовательно, x = -5 — это ответ.

СЛУЧАЙ 2: Когда b положительно, а c отрицательно

Пример 6

Решите x ² + 4x — 5 = 0

Решение

Запишите множители -5.

1 × –5, –1 × 5

Определите факторы, произведение которых равно — 5, а сумма равна 4.

1 — 5 ≠ 4
–1 + 5 = 4

Проверьте факторы, используя свойство распределения.

(x — 1) (x + 5) = x ² + 5x — x — 5 = x ² + 4x — 5
(x — 1) (x + 5) = 0

x — 1 = 0 ⇒ x = 1 или
x + 5 = 0 ⇒ x = -5

Следовательно, x = 1, x = -5 — решения.

ВАРИАНТ 3: Когда b и c отрицательны

Пример 7

x ² — 5x — 6

Решение

Запишите множители — 6:

1 × –6, –1 × 6, 2 × –3, –2 × 3

Теперь определите факторы, произведение которых равно -6, а сумма равна –5:

1 + (–6) = –5

Проверьте коэффициенты используя распределительное свойство.

(x + 1) (x — 6) = x ² — 6 x + x — 6 = x ² — 5x — 6

Приравнять каждый множитель к нулю и решить, чтобы получить;
(x + 1) (x — 6) = 0

x + 1 = 0 ⇒ x = -1, или
x — 6 = 0 ⇒ x = 6

Следовательно, решение x = 6, x = -1

СЛУЧАЙ 4: Когда b отрицательно, а c положительно

Пример 8

x ² — 6x + 8 = 0

Решение

Запишите все множители 8 .

–1 × — 8, –2 × –4

Определите факторы, произведение которых равно 8, а сумма равна -6
–1 + (–8) ≠ –6
–2 + (–4) = –6

Проверьте коэффициенты с помощью распределительного свойства.

(x — 2) (x — 4) = x ² — 4 x — 2x + 8 = x ² — 6x + 8

Теперь приравняйте каждый множитель к нулю и решите выражение, чтобы получить;

(x — 2) (x — 4) = 0

x — 2 = 0 ⇒ x = 2 или
x — 4 = 0 ⇒ x = 4

Пример 9

Разложить на множители x ² + 8x + 12.

Решение

Запишите множители 12;

12 = 2 × 6 или = 4 × 3
Найдите множители, сумма которых равна 8:

2 + 6 = 8
2 × 6 ≠ 8

Используйте свойство распределения, чтобы проверить множители;

= x ² + 6x + 2x + 12 = (x ² + 6x) + (2x + 12) = x (x + 6) +2 (x + 6)

= x (x + 6 ) +2 (x + 6) = (x + 6) (x + 2)

Приравняем каждый множитель к нулю, чтобы получить;

(x + 6) (x + 2)

x = -6, -2

Факторинг, когда коэффициент x

² больше 1

Иногда старший коэффициент квадратного уравнения может быть больше чем 1.В этом случае мы не можем решить квадратное уравнение, используя общие множители.

Следовательно, нам нужно рассмотреть коэффициент при x ² и множители при c, чтобы найти числа, сумма которых равна b.

Пример 10

Решите 2x ² — 14x + 20 = 0

Решение

Определите общие множители уравнения.

2x ² — 14x + 20 ⇒ 2 (x ² — 7x + 10)

Теперь мы можем найти множители (x ² — 7x + 10).Поэтому запишите коэффициенты 10:

–1 × –10, –2 × –5

Определите коэффициенты, сумма которых равна — 7:

1 + (–10) ≠ –7
–2 + (–5) = –7

Проверьте коэффициенты, применив свойство распределения.

2 (x — 2) (x — 5) = 2 (x ² — 5 x — 2x + 10)
= 2 (x ² — 7x + 10) = 2x ² — 14x + 20

Приравняйте каждый множитель к нулю и решите;
2 (x — 2) (x — 5) = 0

x — 2 = 0 ⇒ x = 2 или
x — 5 = 0 ⇒ x = 5

Пример 11

Решить 7x ² + 18x + 11 = 0

Решение

Запишите множители 7 и 11.

7 = 1 × 7

11 = 1 × 11

Примените свойство распределения для проверки факторов, как показано ниже:

(7x + 1) (x + 11) ≠ 7x ² + 18x + 11

(7x + 11) (x + 1) = 7x ² + 7x + 11x + 11 = 7x ² + 18x + 11

Теперь приравняйте каждый множитель к нулю и решите, чтобы получить;

7x ² + 18x + 11 = 0
(7x + 11) (x + 1) = 0

x = -1, -11/7

Пример 12

Решить 2x ² — 7x + 6 = 3

Решение

2x ² — 7x + 3 = 0

(2x — 1) (x — 3) = 0

x = 1/2 или x = 3

Пример 13

Решить 9x ² + 6x + 1 = 0

Решение

Разложите на множители, чтобы получить:

(3x + 1) (3x + 1) = 0

(3x + 1) = 0,

Следовательно, x = −1 / 3

Пример 14

Разложить на множители 6x ² — 7x + 2 = 0

Решение

6x ² — 4x — 3x + 2 = 0

Разложите выражение на множители;

⟹ 2x (3x — 2) — 1 (3x — 2) = 0

⟹ (3x — 2) (2x — 1) = 0

⟹ 3x — 2 = 0 или 2x — 1 = 0

⟹ 3x = 2 или 2x = 1

⟹ x = 2/3 или x = ½

Пример 15

Факторизация x ² + (4 — 3y) x — 12y = 0

Решение

Разверните уравнение;

x ² + 4x — 3xy — 12y = 0

Разложить на множители;

⟹ x (x + 4) — 3y (x + 4) = 0

x + 4) (x — 3y) = 0

⟹ x + 4 = 0 или x — 3y = 0

⟹ x = -4 или x = 3y

Таким образом, x = -4 или x = 3y

Практические вопросы

Решите следующие квадратные уравнения путем факторизации:

1. 3x ² -20 = 160 — 2x ²
2. (2x — 3) ² = 49
3. 16x ² = 25
4. (2x + 1) ² + (x + 1) ² = 6x + 47
5. 2x ² + x — 6 = 0
6. 3x ² = x + 4
7. (x — 7) (x — 9) = 195
8. x ² — (a + b) x + ab = 0
9. x ² + 5 x + 6 = 0
10. x ² -2 x — 15 = 0

Ответы

1. 6, -6
2. -2, 5
3. — 5/4, 5/4
4. -3, 3
5. -2, 3/2
6. -1 , 4/3
7. -6, 22
8. a, b
9. –3, –2
10. 5, — 3

Предыдущий урок | Главная страница | Следующий урок

Что такое факторинг? Определение и примеры

Факторинг — это вид финансирования, при котором одна компания покупает дебиторскую задолженность другой компании , т. е.е., его счета-фактуры (деньги, которые ему причитаются). Когда продавец отправляет своему покупателю счет, факторинговая компания немедленно выплачивает продавцу от 70% до 85% стоимости счета. Продавец получает остаток, когда покупатель оплачивает счет. Клиент оплачивает счет факторинговой компании.

Эта форма финансирования помогает предприятиям сталкиваться с проблемами движения денежных средств из-за медленно платящих клиентов. Финансируя свои счета-фактуры, компания, испытывающая проблемы с денежным потоком, имеет оборотных средств

Денежный поток — это движение денег в компанию, организацию или счет и из них.

В алгебре «факторинг» (UK: факторизация) — это процесс нахождения множителей числа. Например, в уравнении 2 x 3 = 6 числа два и три являются множителями.

Эта статья посвящена значению этого термина в мире бизнеса и финансов.

Team Technology имеет следующее определение термина:

«[Факторинг] — это продажа ваших счетов факторинговой компании. Вы получаете наличные быстро, и вам не нужно взыскивать долг.”

«Однако вы теряете часть стоимости счета. Факторинговая компания получает долг и должна его взыскать ».

Компания, покупающая ваши счета, зарабатывает деньги, взимая с вас процент от стоимости счета. Мы называем компанию, которая покупает ваши счета, «, фактор ».

По данным ООО «Коммерческий капитал»: «Ставки обычно колеблются от 1,5% до 4,5% за 30 дней. Авансы обычно составляют от 70% до 85%. Есть некоторые исключения, такие как транспорт и укомплектование персоналом, где авансы могут достигать или превышать 90%.”

Факторинг против дисконтирования по счету

Не путайте термин с дисконтом по счету. При дисконтировании счета компания запрашивает ссуду и использует свою дебиторскую задолженность в качестве обеспечения. Однако при факторинге компания продает свою дебиторскую задолженность.

В Соединенном Королевстве разница между этими двумя терминами не так очевидна.

На некоторых рынках Великобритании люди рассматривают дисконтирование счетов как одну из форм факторинга. В частности, когда это связано с «уступкой дебиторской задолженности» в статистике факторинга.

Что касается значения дисконтирования счетов в Великобритании, Википедия пишет:

«Следовательно, это также не считается заимствованием в Великобритании. В Великобритании договоренность обычно носит конфиденциальный характер, поскольку должник не уведомляется об уступке дебиторской задолженности, а продавец дебиторской задолженности взыскивает задолженность от имени фактора ».

«В Великобритании основное различие между факторингом и дисконтированием счетов — конфиденциальность».

Факторинг за и против

Плюсы

— Деньги получаются быстро.

— Меньше хлопот. Фактор предполагает все хлопоты по контролю за кредитом, то есть погоню за безнадежными долгами. Впоследствии вы можете высвободить свое и других людей время для ведения бизнеса.

Безнадежный долг — это просроченный платеж, который либо никогда не будет выплачен, либо потребует решительных действий. Кредитору, возможно, придется подать на должника в суд. Должником является песон или сторона, которая должна деньги.

— Вы можете лучше контролировать движение денежных средств в компании. Это также упрощает планирование заранее.

— Клиенты склонны уважать факторы. Поэтому они с большей вероятностью заплатят вовремя.

— Если вы выберете факторинг без права регресса, вам не придется беспокоиться о безнадежных долгах.

— Ваш фактор будет проверять кредитоспособность ваших клиентов. Это может гарантировать, что вы ведете бизнес с хорошими клиентами.

Минусы

— Фактор получает процент от стоимости вашего счета. Следовательно, страдает ваша маржа прибыли.

— Вы потеряете некоторую гибкость.Вы должны вести дела с компаниями, одобренными фактором.

— Согласно BIBusinessInfo. co.uk: «Запросы и споры могут отрицательно повлиять на ваше доступное финансирование. По этой причине факторинг работает лучше всего, когда бизнес эффективен, а споров и запросов мало ».

— Некоторым вашим клиентам могут не нравиться кредитные контролеры фактора, то есть погонщики за долгами.

— Риск сложения. Согласно Byte Start , «быстрое получение денег» похоже на наркотик.Сойти с него может быть нелегко. Например, вам может потребоваться вливание капитала, чтобы получить бесплатное.

FinanceExpert содержит интересную информацию о факторинге. На его веб-сайте объясняется, что это такое, как это работает и как компании могут этим воспользоваться. Это также говорит нам, каковы затраты.

Видео — Что такое кредитный контроль?

Что такое фактор? [Определение, факты и пример]

Что такое факторы?

Умножение двух целых чисел дает произведение. Числа, которые мы умножаем, являются множителями продукта.

Пример : 3 × 5 = 15, следовательно, 3 и 5 являются множителями 15.

Это также означает:

Коэффициент делит число полностью, не оставляя остатка.

Например, : 30 ÷ 6 = 5, и остатка нет. Таким образом, мы можем сказать, что 5 и 6 являются множителями 30.

В данном примере мы можем дополнительно разбить или упростить число 6 на его множители, то есть 2 и 3.Другими словами, когда мы умножаем 5, 2 и 3, мы все равно получаем 30. Следовательно, множители 30 равны 5, 2 и 3. Кроме того, 5 × 2 = 10. Таким образом, 10 также является множителем 30. Точно так же 5 × 3 = 15. Итак, 15 также является множителем 30. Наконец, множители 30 равны 1, 2, 3, 5, 6, 10, 15 и 30

.

• Число 1 — наименьший делитель каждого числа.

• Каждое число будет иметь как минимум два множителя: 1 и само число.

• Число, состоящее только из двух делителей, 1 и самого числа, называется простым числом.

Факторизация на простые множители

• Когда мы записываем число как произведение всех его простых множителей, это называется разложением на простые множители.

• Каждое число в разложении на простые множители является простым числом.

• Иногда, чтобы записать простые множители числа, нам, возможно, придется повторить число.

Интересные факты Множители всегда целые или целые числа и никогда не являются десятичными или дробными. Все четные числа имеют множитель 2. Все числа, оканчивающиеся на 5, будут иметь множитель 5. Все числа больше 0 и оканчивающиеся на 0 будут иметь множители 2, 5 и 10. Алгебраические выражения часто решаются или упрощаются с помощью факторизации.

Разложите многочлен или выражение на множители с помощью программы «Пошаговое решение математических задач

»

Процесс факторизации необходим для упрощения многих алгебраических выражений и является полезным инструментом при решении уравнений более высокой степени.Фактически, процесс факторизации настолько важен, что очень мало алгебры, выходящей за рамки этого пункта, может быть достигнуто без понимания этого.

В предыдущих главах подчеркивалось различие между терминами и факторами . Вы должны помнить, что члены складываются или вычитаются, а множители умножаются. Далее следуют три важных определения.

Термины встречаются в указанной сумме или разнице. Факторы встречаются в указанном продукте.

Выражение в факторизованной форме только в том случае, если все выражение является указанным продуктом.

Обратите внимание, что в этих примерах мы всегда должны рассматривать все выражение целиком. Факторы могут состоять из терминов, а термины могут содержать факторы, но факторизованная форма должна соответствовать приведенному выше определению.

Факторинг — это процесс преобразования выражения суммы или разности членов в произведение факторов.

Обратите внимание, что в этом определении подразумевается, что значение выражения не изменяется — изменяется только его форма.

УДАЛЕНИЕ ОБЩИХ ФАКТОРОВ

ЦЕЛИ

По завершении этого раздела вы сможете:

1. Определите, какие факторы являются общими для всех терминов в выражении.
2. Фактор общие множители.

В предыдущей главе мы умножили такое выражение, как 5 (2x + 1), чтобы получить 10x + 5. В общем, факторинг «отменит» умножение. Каждый член 10x + 5 имеет множитель 5, а 10x + 5 = 5 (2x + 1).

Чтобы разложить выражение на множители путем удаления общих множителей, действуйте, как в примере 1.

3x — наибольший общий делитель всех трех членов.

Затем найдите факторы, общие для всех терминов, и найдите наибольший из них. Это самый общий фактор. В этом случае наибольший общий множитель равен 3x.

Поставьте 3x перед круглыми скобками.

Термины в круглых скобках находятся путем деления каждого члена исходного выражения на 3x.

Обратите внимание, что это свойство распределения. Это процесс, обратный тому, что мы использовали до сих пор.

Исходное выражение теперь преобразовано в факторизованную форму. Чтобы проверить факторинг, имейте в виду, что факторинг изменяет форму, но не значение выражения. Если ответ правильный, это должно быть правдой. Умножьте, чтобы убедиться, что это правда. Вторая проверка также необходима для факторинга — мы должны быть уверены, что выражение было полностью факторизовано.Другими словами, «Удали ли мы все общие факторы? Можем ли мы использовать дополнительные факторы?»

Если бы мы только удалили множитель «3» из 3x ² + 6xy + 9xy ² , ответ был бы

3 (х ² + 2xy + 3xy ² ).

Перемножая для проверки, мы обнаруживаем, что ответ фактически совпадает с исходным выражением. Однако фактор x по-прежнему присутствует во всех терминах. Следовательно, выражение не учитывается полностью.

Это выражение факторизовано, но не полностью.

Чтобы факторинг был правильным, решение должно соответствовать двум критериям:

1. Должна быть возможность умножить факторизованное выражение и получить исходное выражение.
2. F Выражение должно быть полностью разложено на множители .

Пример 2 Фактор 12x ³ + 6x ² + 18x.

Решение

На этом этапе нет необходимости перечислять факторы каждого семестра.Вы должны уметь мысленно определить наиболее общий фактор. Хорошая процедура для подражания — думать об элементах по отдельности. Другими словами, не пытайтесь получить все общие множители сразу, а получите сначала число, а затем каждую задействованную букву. Например, 6 — множитель 12, 6 и 18, а x — множитель каждого члена. Следовательно, 12x ³ + 6x ² + 18x = 6x (2x ² + x + 3). Умножая, мы получаем оригинал и видим, что члены в круглых скобках не имеют другого общего множителя, поэтому мы знаем, что решение правильное.

Скажите себе: «Каков наибольший общий делитель 12, 6 и 18?»

Затем «Какой наибольший общий делитель x 3 , x 2 и x?»

Помните, это проверка, чтобы убедиться, что мы правильно разложили на множители.

Опять умножаем как чек.

Снова найдите наибольший общий делитель чисел и каждой буквы отдельно.

Если выражение не может быть разложено на множители, оно называется простым .

Помните, что 1 всегда является множителем любого выражения.

РАЗДЕЛЕНИЕ ПО ГРУППАМ

ЦЕЛИ

По завершении этого раздела вы сможете:

1. Факторные выражения, когда общий множитель включает более одного члена.
2. Фактор по группировке.

Расширение идей, представленных в предыдущем разделе, применяется к методу факторинга, называемому группировка .

Прежде всего мы должны отметить, что общий множитель не обязательно должен быть одним членом. Например, в выражении 2y (x + 3) + 5 (x + 3) есть два члена. Это 2y (x + 3) и 5 ​​(x + 3). В каждом из этих терминов есть множитель (x + 3), состоящий из членов. Этот множитель (x + 3) является общим множителем.

Иногда, когда имеется четыре или более терминов, мы должны вставить один или два промежуточных шага, чтобы разложить их на множители.

Решение

Прежде всего отметьте, что не все четыре члена в выражении имеют общий множитель, но некоторые из них имеют.Например, мы можем умножить на 3 первые два члена, получив 3 (ax + 2y). Если мы вычленим a из оставшихся двух членов, мы получим a (ax + 2y). Выражение теперь 3 (ax + 2y) + a (ax + 2y), и у нас есть общий множитель (ax + 2y), и мы можем разложить на множители как (ax + 2y) (3 + a). Умножая (ax + 2y) (3 + a), мы получаем исходное выражение 3ax + 6y + a ² x + 2ay и видим, что факторизация верна.

Это пример факторинга путем группировки , поскольку мы «сгруппировали» термины по два за раз.

Умножьте (x — y) (a + 2) и посмотрите, получите ли вы исходное выражение. Опять умножаем как чек.

Иногда термины необходимо сначала переставить, прежде чем можно будет выполнить факторинг по группировке.

Пример 7 Фактор 3ax + 2y + 3ay + 2x.

Решение

Первые два члена не имеют общего множителя, но первое и третье члены имеют, поэтому мы перегруппируем члены, поместив третий член после первого.Всегда смотрите вперед, чтобы увидеть порядок, в котором можно было бы расположить термины.

Во всех случаях важно убедиться, что факторы, указанные в скобках, абсолютно одинаковы. Это может потребовать факторизации отрицательного числа или буквы.

Помните, свойство коммутативности позволяет нам переставлять эти члены. Умножение как проверка.

Пример 8 Фактор ax — ay — 2x + 2y.

Решение

Обратите внимание, что когда мы множим a из первых двух членов, мы получаем a (x — y).Глядя на последние два члена, мы видим, что разложение на множители +2 дает 2 (-x + y), а разложение на множители «-2» дает -2 (x — y). Мы хотим, чтобы члены в круглых скобках были (x — y), поэтому поступаем таким же образом.

ФАКТОР ТРИНОМИАЛОВ

ЦЕЛИ

По завершении этого раздела вы сможете:

1. Мысленно перемножьте два бинома.
2. Разложите на множители трехчлена с коэффициентом первого члена, равным 1.
3. Найдите множители любого факторизуемого трехчлена.

Большое количество будущих задач будет включать факторизацию трехчленов как произведения двух биномов. В предыдущей главе вы узнали, как умножать многочлены. Теперь мы хотим рассмотреть частный случай умножения двух биномов и разработать образец для этого типа умножения.

Поскольку этот тип умножения очень распространен, полезно иметь возможность найти ответ, не проделывая столько шагов. Давайте посмотрим на образец для этого.

Из примера (2x + 3) (3x — 4) = 6x ² + x — 12, обратите внимание, что первый член ответа (6x ² ) был получен из произведения двух первых членов множителей. , то есть (2x) (3x).

Также обратите внимание, что третий член (-12) произошел от произведения вторых членов множителей, то есть (+ 3) (- 4).

Теперь у нас есть следующая часть узора:

Теперь, снова посмотрев на пример, мы видим, что средний член (+ x) получен из суммы двух произведений (2x) (-4) и (3) (3x).

Для любых двух биномов у нас теперь есть эти четыре произведения:

1. Первый семестр по первый семестр
2. Внешние условия
3. Внутренние условия
4. Последний семестр к последнему семестру

Эти продукты показаны этим шаблоном.

Когда произведения внешних и внутренних терминов дают одинаковые термины, их можно комбинировать, и решение является трехчленом.

Этот метод умножения двух биномов иногда называют методом FOIL. FOIL расшифровывается как First, Outer, Inner, Last. Это сокращенный метод умножения двух биномов, и его полезность станет очевидной, когда мы разложим на множители трехчлены.

Вы должны запомнить этот образец.

Опять же, возможно, вам поможет запоминание слова FOIL.

Не только этот образец должен быть запомнен, но ученик также должен научиться переходить от проблемы к ответу без каких-либо письменных шагов.Этот умственный процесс умножения необходим, если мы хотим достичь мастерства в факторинге.

Выполняя следующие упражнения, попытайтесь прийти к правильному ответу, не записывая ничего, кроме ответа. Чем больше вы будете практиковать этот процесс, тем лучше вы будете в факторинге.

Теперь, когда мы установили образец умножения двух биномов, мы готовы разложить на множители трехчлены. Сначала мы рассмотрим факторизацию только тех трехчленов с коэффициентом первого члена, равным 1.

Решение

Так как это трехчлен и не имеет общего множителя, мы будем использовать шаблон умножения для факторизации.

Фактически мы будем работать в обратном порядке, как в предыдущем наборе упражнений.

Сначала укажите проблему в скобках.

Теперь мы хотим заполнить члены так, чтобы шаблон давал исходный трехчлен при умножении. Первый член прост, поскольку мы знаем, что (x) (x) = x ² .

Помните, произведение первых двух членов бинома дает первый член трехчлена.

Теперь мы должны найти числа, которые умножаются, чтобы получить 24, и в то же время складывать, чтобы получить средний член. Обратите внимание, что в каждом из следующих слов будут правильные первый и последний член.

Только последний продукт имеет средний член 11x, и правильное решение —

Этот метод факторинга называется методом проб и ошибок — по понятным причинам.

Здесь могут быть полезны некоторые числовые факты из арифметики. Произведение двух нечетных чисел является нечетным. Произведение двух четных чисел четное. Произведение четного и нечетного числа — четное. Сумма двух нечетных чисел четная. Сумма двух четных чисел четная. Сумма нечетного и четного числа нечетна. Следовательно, когда мы разлагаем на множители такое выражение, как x 2 + 11x + 24, мы знаем, что произведение двух последних членов в биномах должно быть 24, что является четным, и их сумма должна быть 11, что является нечетным. Таким образом, будут работать только нечетное и четное число. Нам даже не нужно пробовать такие комбинации, как 6 и 4 или 2 и 12 и так далее.

Решение

Здесь проблема лишь немного в другом. Мы должны найти числа, которые умножаются, чтобы получить 24, и в то же время складывать, чтобы получить — 11. Вы всегда должны помнить об этой схеме. Последний член получается строго умножением, а средний член получается, наконец, из суммы. Зная, что произведение двух отрицательных чисел положительно, а сумма двух отрицательных чисел отрицательна, получаем

Решение

Здесь мы столкнулись с отрицательным числом для третьего члена, и это немного усложняет задачу.Поскольку -24 может быть только произведением положительного числа и отрицательного числа, и поскольку средний член должен происходить из суммы этих чисел, мы должны мыслить категориями разницы. Мы должны найти числа, произведение которых равно 24 и которые отличаются на 5. Кроме того, большее число должно быть отрицательным, потому что, когда мы складываем положительное и отрицательное число, ответ будет иметь знак большего. Учитывая все это, получаем

Порядок коэффициентов несущественный. по коммутативному закону умножения.

Следующие пункты помогут при факторизации трехчленов:

1. Когда знак третьего члена положительный, оба знака в множителях должны быть одинаковыми — и они должны быть похожи на знак среднего члена.
2. Когда знак последнего члена отрицательный, знаки в множителях должны быть разными, а знак большего члена должен быть подобен знаку среднего члена.

В предыдущем упражнении коэффициент каждого из первых членов был равен 1.Когда коэффициент при первом члене не равен 1, проблема факторинга намного сложнее, потому что количество возможностей значительно увеличивается.

Выполнив предыдущий набор упражнений, теперь вы готовы попробовать еще несколько сложных трехчленов.

Обратите внимание, что существует двенадцать способов получить первый и последний члены, но только один имеет 17x в качестве среднего члена.

Вы, конечно, можете попробовать каждый из них мысленно, вместо того, чтобы записывать их.

Есть только один способ получить все три условия:

В этом примере верна одна из двенадцати возможностей. Таким образом, метод проб и ошибок может занять очень много времени.

Даже несмотря на то, что используемый метод представляет собой метод угадывания, это должно быть «обоснованное предположение», в котором мы применяем все наши знания о числах и упражняемся в умственной арифметике. В предыдущем примере мы сразу отбросили бы многие комбинации.Поскольку мы ищем 17x как средний термин, мы не будем пытаться использовать те возможности, которые умножают 6 на 6, или 3 на 12, или 6 на 12, и так далее, поскольку эти произведения будут больше 17. Кроме того, поскольку 17 нечетное, мы знаем, что это сумма четного и нечетного числа. Все это помогает сократить количество попыток.

Сначала найдите числа, которые дают правильные первое и последнее члены трехчлена. Затем добавьте внешний и внутренний продукт, чтобы проверить правильность среднего срока.

Решение

Сначала мы должны проанализировать проблему.

1. Последний член положительный, поэтому два одинаковых знака.
2. Средний член отрицательный, поэтому оба знака будут отрицательными.
3. Множители 6×2: x, 2x, 3x, 6x. Множители 15: 1, 3, 5, 15.
4. Исключите как слишком большое произведение 15 на 2x, 3x или 6x. Попробуйте несколько разумных комбинаций.

Это автоматически даст слишком большой средний член.

Посмотрите, как сокращается количество возможностей.

Решение

Анализировать:

1. Последний член отрицательный, поэтому не похож на знаки.
2. Мы должны найти продукты, которые отличаются на 5, а большее число отрицательно.
3. Мы исключаем произведение 4х и 6 как вероятно слишком большое.
4. Попробуйте несколько комбинаций.

Помните, попробуйте мысленно различные возможные комбинации, которые являются разумными.Это процесс факторинга «методом проб и ошибок». Практикуясь, вы станете более опытным в этом процессе.

(4x — 3) (x + 2): здесь средний член равен + 5x, что является правильным числом, но неправильным знаком. Будьте осторожны, чтобы не принимать это как решение, но поменяйте знаки так, чтобы более крупный продукт соответствовал знаку со средним условием.

К тому времени, когда вы закончите следующий набор упражнений, вы почувствуете себя намного более комфортно при факторинге трехчлена.

ОСОБЫЕ СЛУЧАИ ФАКТОРИНГА

ЦЕЛИ

По завершении этого раздела вы сможете:

1. Определите и разложите на множители двух полных квадратов.
2. Определите и разложите на множители трехчлен полного квадрата.

В этом разделе мы хотим изучить некоторые частные случаи факторинга, которые часто возникают в задачах. Если признать эти особые случаи, факторинг значительно упростится.

Первый частный случай, который мы обсудим, — это разность двух полных квадратов .

Напомним, что при умножении двух биномов на образец средний член получается из суммы двух произведений.

Из нашего опыта работы с числами мы знаем, что сумма двух чисел равна нулю только в том случае, если два числа являются отрицательными по отношению друг к другу.

Когда сумма двух чисел равна нулю, одно из чисел называется , аддитивно инверсным другого. Например: (+ 3) + (-3) = 0, поэтому + 3 является аддитивным обратным значением — 3, также -3 — аддитивным обратным значением +3.

В каждом примере средний член равен нулю. Обратите внимание, что если два бинома умножаются, чтобы получить бином (средний член отсутствует), они должны быть в форме (a — b) (a + b).

Правило можно записать как = (a — b) (a + b). Это форма, которую вы найдете наиболее полезной при факторинге.

Чтение этого правила справа налево говорит нам, что если у нас есть проблема, которую нужно разложить на множители, и если она имеет форму, то множители будут (a — b) (a + b).

Решение

Здесь оба члена представляют собой полные квадраты, разделенные знаком минус.

Особые случаи действительно облегчают факторинг, но не забывайте понимать, что особый случай — это просто особенный случай. В этом случае оба члена должны быть полными квадратами, а знак должен быть отрицательным, отсюда «разница двух полных квадратов».

Сумму двух квадратов нельзя разложить на множители.

Вы также должны быть осторожны при распознавании идеальных квадратов.Помните, что точные квадратные числа — это числа, у которых квадратные корни являются целыми числами. Кроме того, показатели абсолютного квадрата четны.

Студенты часто упускают из виду тот факт, что (1) — это идеальный квадрат. Таким образом, такое выражение, как x 2 — 1, представляет собой разность двух полных квадратов и может быть разложено на множители этим методом.

Другой частный случай факторизации — это трехчлен полного квадрата. Обратите внимание, что возведение бинома в квадрат приводит к этому случаю.

Мы признаем этот случай по его особенностям. Очевидны три вещи.

1. Первый член — это полный квадрат.
2. Третий член представляет собой полный квадрат.
3. Средний член — это дважды произведение квадратного корня из первого и третьего членов.

Для факторинга более полезно записать отчет как

Решение

1. 25x ² — это полный квадратный корень с главным квадратным корнем = 5x.
2. 4 — точный квадратный корень из главного квадрата = 2.
3. 20x — это дважды произведение квадратных корней 25x ² и
4. 20x = 2 (5x) (2).

Чтобы разложить на множители полный квадрат трехчлена , сформируйте бином с квадратным корнем из первого члена, квадратным корнем из последнего члена и знаком среднего члена и укажите квадрат этого бинома.

Таким образом, 25x ² + 20x + 4 = (5x + 2) ²

Всегда возводите двучлен в квадрат для проверки правильности среднего члена.

Не частный случай трехчлена полного квадрата.

ДОПОЛНИТЕЛЬНЫЕ БЛОКИРОВКИ ДЛЯ ИСПЫТАНИЙ И ФАКТОРИРОВАНИЯ ОШИБОК

ЦЕЛИ

По завершении этого раздела вы сможете:

1. Найдите ключевое число трехчлена.
2. Используйте ключевое число для разложения трехчлена на множители.

В этом разделе мы хотим обсудить некоторые сокращения факторинга методом проб и ошибок. Это необязательно по двум причинам. Во-первых, некоторые могут предпочесть пропустить эти методы и просто использовать метод проб и ошибок; во-вторых, эти ярлыки не всегда практичны для большого количества людей.Однако они повысят скорость и точность для тех, кто их освоит.

Первым шагом в использовании этих ярлыков является поиск номера ключа . После того, как вы нашли ключевой номер, его можно использовать более чем одним способом.

В трехчлене, подлежащем разложению, ключевое число является произведением коэффициентов первого и третьего членов.

Произведение этих двух чисел является «ключевым числом».

Первое использование номера ключа показано в примере 3.

Решение
Шаг 1 Найдите ключевой номер. В этом примере (4) (- 10) = -40.
Шаг 2 Найдите множители ключевого числа (-40), которые складываются, чтобы получить коэффициент среднего члена (+ 3). В этом случае (+ 8) (-5) = -40 и (+ 8) + (-5) = +3.
Шаг 3 Коэффициенты (+ 8) и (- 5) будут перекрестными произведениями в шаблоне умножения.

Произведение этих двух чисел является ключевым числом.»

Шаг 4 Используя только внешнее перекрестное произведение, найдите множители первого и третьего членов, которые будут умножаться, чтобы дать произведение. В этом примере мы должны найти множители 4×2 и -10, которые будут умножаться, чтобы дать + 8x. Это 4x от 4×2 и (+ 2) от (-10).
Поместите эти факторы в первую и последнюю позиции в шаблоне

Есть только один способ сделать это правильно.

Шаг 5 Забудьте на этом этапе номер ключа и посмотрите на исходную проблему.Поскольку первая и последняя позиции заполнены правильно, теперь необходимо заполнить только две другие позиции.

Опять же, это можно сделать только одним способом.

Мы знаем, что произведение двух первых членов должно давать 4x ² и 4x уже на месте. Нет другого выбора, кроме x.

Обратите внимание, что на шаге 4 мы могли бы начать с внутреннего продукта вместо внешнего продукта. Мы получили бы те же множители.Самое главное — иметь систематический процесс факторинга.

Мы знаем, что произведение двух вторых членов должно быть (-10), а (+ 2) уже на месте. У нас нет другого выбора, кроме (- 5).

Помните, что если трехчлен факторизуем, существует только один возможный набор факторов.

Если не удается найти множители ключевого числа, сумма которых является коэффициентом средних членов, то трехчлен является простым и не множится.

Второе использование номера ключа в качестве ярлыка включает факторинг по группировке. Работает как в примере 5.

Решение
Шаг 1 Найдите номер ключа (4) (- 10) = -40.
Шаг 2 Найдите множители (- 40), которые добавят к коэффициенту среднего члена (+3).

Шаги 1 и 2 в этом методе такие же, как и в предыдущем методе.

Шаг 3 Перепишите исходную задачу, разбив средний член на две части, найденные на шаге 2.8x — 5x = 3x, поэтому мы можем написать

Step 4 Разложите эту проблему на множители, начиная с шага 3, с помощью метода группировки, изученного в разделе 8-2

Теперь это становится обычным факторингом с помощью задачи группировки.

Следовательно,

Опять же, есть только одна возможная пара множителей, которая может быть получена из данного трехчлена.

Помните, что если шаг 2 невозможен, трехчлен является простым и не может быть разложен на множители.

ПОЛНАЯ ФАКТОРИЗАЦИЯ

ЦЕЛИ

По завершении этого раздела вы сможете разложить на множители трехчлен, выполнив следующие два шага:

1. Сначала найдите общие факторы.
2. Разложите оставшийся трехчлен на множители, применяя методы этой главы.

Теперь мы изучили все обычные методы факторизации в элементарной алгебре. Однако вы должны знать, что для решения одной проблемы может потребоваться более одного из этих методов.Помните, что есть две проверки правильности факторинга.

1. Умножатся ли множители, чтобы получить исходную задачу?
2. Все ли факторы просты?

После того, как общий множитель был найден, вы должны проверить, можно ли факторизовать полученный трехчлен.

Если у трехчлена есть общие множители, обычно проще, если они сначала разложены на множители.

Хорошая процедура, которой следует придерживаться при факторинге, — всегда сначала удалять наибольший общий множитель, а затем, если возможно, разложить на множители то, что осталось.

СВОДКА

Ключевые слова

• Выражение в факторизованной форме только в том случае, если все выражение является указанным продуктом.
• Факторинг — это процесс, который изменяет сумму или разность условий на произведение факторов.
• Простое выражение не может быть разложено на множители.
• Наибольший общий множитель является наибольшим общим множителем для всех терминов.
• Выражение полностью разложено на множители , когда дальнейшее разложение на множители невозможно.
• Возможность разложения на множители путем группирования существует, когда выражение содержит четыре или более терминов.
• Метод FOIL можно использовать для умножения двух биномов.
• Частные случаи факторинга включают разность двух квадратов и трехчленов полного квадрата .
• Ключевой номер является произведением коэффициентов первого и третьего членов трехчлена.

Процедуры

• Чтобы удалить общие множители, найдите наибольший общий делитель и разделите на него каждый член.
• Триномы можно разложить на множители методом проб и ошибок. При этом используется шаблон умножения, чтобы найти факторы, которые дадут исходный трехчлен.
  
• Чтобы разложить на множитель разность двух квадратов, используйте правило
  
• Чтобы разложить на множители полный квадрат трехчлена, сформировать двучлен с квадратным корнем из первого члена, квадратным корнем из последнего члена и знаком среднего члена и указать квадрат этого бинома.
• Используйте ключевое число как вспомогательное средство для определения факторов, сумма которых является коэффициентом среднего члена трехчлена.2} термин, потому что он понят.

  Если вы готовы принять вызов, у меня есть еще один урок по факторингу трехчлена, в котором абсолютное значение ведущего коэффициента не равно 1. Это называется факторинг трехчленов («Жесткий случай»). Поверьте, это не так уж и сложно. Вам просто нужно будет выполнить дополнительные шаги.

  Таким образом, общий вид «легкого» дела сводится к

  Простой случай трехчлена

  Основная стратегия факторизации этого типа трехчлена состоит в том, чтобы найти два числа (факторная пара), которые при умножении дают постоянное число c.2 + 7x + 10 как произведение двух биномов.

  Очевидно, это «легкий» случай, потому что коэффициент при квадрате члена x равен 1. Это здорово! Теперь мы можем сосредоточиться на шагах, чтобы это исключить.

  В этом трехчлене нам нужно определить другие соответствующие константы. Обратите внимание, что b = 7 и c = 10 . Ознакомьтесь с перепиской ниже.

  Затем найдите два числа (пару факторов), которые при умножении равны постоянному значению c = 10, а при сложении равны постоянному значению b = 7.Поскольку произведение двух чисел должно быть положительным, оба числа должны быть положительными или отрицательными.

  Чтобы найти пару, вы можете выполнить несколько проб и ошибок, чтобы найти правильную комбинацию. Вот несколько возможных комбинаций.

  Единственная комбинация чисел, которая может удовлетворить двум данным требованиям, — это третий вариант. Тот, который отмечен зеленой галочкой , . Наконец, мы можем выразить биномиальные множители этого трехчлена, записав пару скобок с x в качестве ведущего члена.2-2x-15 как произведение двух биномов.

  Коэффициент при квадрате члена равен 1, так что это должен быть «легкий» случай. Теперь нам нужно найти два числа, которые при умножении дают последнюю константу (c = -15), а при сложении дают среднюю константу (b = -2). 2-9x + 14 на множители как произведение двух биномов.

  В этом случае два числа должны иметь произведение c = 14 и сумму b = -9. Это означает, что числа должны иметь одинаковый знак, положительный или отрицательный. Однако, поскольку сумма двух чисел отрицательна, мы можем сказать, что пара также должна быть отрицательной.

  Путем проб и ошибок возможных комбинаций

  Так как пара –7 и –2 удовлетворяет условиям, наш факторизованный трехчлен выглядит так.2 + 13x + 12 как произведение двух двучленов.

  Решение:

  Мне нужно найти два числа, произведение которых (при умножении) равняется 12 , а их сумма (при сложении) равна 13 .

  Правильная комбинация должна быть 12 и 1 . Почему?

  Это потому, что произведение и сумма равны 12 и 13, соответственно, которые идеально соответствуют коэффициентам трехчлена выше. 2 + 4x-4 как произведение двух биномов.2 равно , равному и 1.

Нам нужно найти два числа, произведение которых равно c = 4, а их сумма равна b = -4.

Это список возможных комбинаций.

Так как пара чисел –2 и –2 удовлетворяет данным условиям, множители будут равны

.

Но не забывайте −1 , которое было исключено вначале! Нам нужно включить это в наш окончательный ответ —

.

---

Практика с рабочими листами

---

Возможно, вас заинтересует:

Разложение на множители трехчлена, где a> 1
Триномиальное разложение на множители с использованием «боксового» метода

Факторинговые многочлены

Факторинг, процесс «неумножения» многочленов с целью возврата к уникальной строке многочленов меньшей степени, произведение которых является исходным многочленом, является самым простым способом решения уравнений более высокой степени.Хотя вы уже должны хорошо разбираться в факторинге, вот методы, с которыми вам следует ознакомиться на случай, если вам понадобится обзор.

Наибольшие общие факторы

Если все члены полинома содержат один или несколько одинаковых множителей, объедините эти похожие множители в один моном, называемый наибольшим общим множителем , и перепишите полином в факторизованной форме.

Пример 1: Разложите выражения на множители.

15 x ³ + 5 x ² −25 x

Поскольку каждый член полинома делится как на x , так и на 5, наибольший общий делитель равен 5 x .В факторизованной форме многочлен записывается как 5 x (3 x ² + x — 5).

18 x ³ y ⁵ z ⁴ + 6 x ² yz ³ — 9 x ² y

8 3 z ²

Наибольший моном, на который каждый из членов делится без остатка, и, следовательно, наибольший общий делитель, равен 3 x ² yz ² , поэтому вычтите его за множитель.

Факторинг по группировке

Иногда наибольший общий фактор выражения — это не просто одночлен, а целая величина в скобках. Вам разрешено вычитать количества в скобках так же, как вы можете вычитать отдельные термины.

Пример 2: Разложите следующие выражения на множители.

3 x ( x — 5) + 2 y ( x — 5) — 10 ( x — 5)

Единственное, что делится на каждый из этих членов равномерно, — это линейное выражение ( x — 5).Вынесите его за скобки, как если бы вы делали любой наибольший общий множитель, оставив одночлен в каждом члене, умноженном на ( x — 5):

3 x ² — 6 x — 4 x + 8

Ничто, кроме числа 1, не делится равномерно на каждое из членов, и нет смысла вычитать 1. Однако первые два члена имеют наибольший общий множитель 3 x . Кроме того, если вынести -4 из последних двух членов, вы можете разложить их по группам:

Факторинг квадратичных трехчленов

Ваша самая распространенная задача разложения на множители, помимо наибольшего общего разложения, — это преобразование квадратного трехчлена в произведение двух линейных двучленов.

Пример 3: Разложите следующие выражения на множители.

x ² — 4 x — 12

Если ведущий коэффициент равен 1, как здесь, процесс прост. Найдите два числа, сумма которых равна коэффициенту при члене x , а произведение которых равно постоянному члену. Единственные два числа, сумма которых равна −4 и которые умножаются, чтобы дать −12, — это −6 и 2. Используйте их как константы в линейных множителях:

x ² -10 x + 24

Так как этот квадратный трехчлен имеет старший коэффициент 1, найдите два числа с произведением 24 и суммой −10.Поэкспериментировав, вы обнаружите, что эти числа равны −6 и −4:

.

2 x ² + 9 x — 5

Если ведущий коэффициент не равен 1, необходимо выполнить другую процедуру. Вы по-прежнему ищете два числа, и эти числа все равно дадут в сумме 9. Однако они умножатся и вы получите −10, произведение ведущего коэффициента и константы. (Вам не нужно было использовать эту технику, когда ведущий коэффициент был равен 1, поскольку произведение ведущего коэффициента и константы в любом случае было бы константой.) Рассматриваемые числа — 10 и -1. Перепишите коэффициент x как сумму этих чисел:

Распределите x как на 10, так и на −1:

До финиша, фактор по группировке:

Шаблоны специальных коэффициентов

Иногда единственное усилие, которое вам придется приложить для решения проблемы факторизации, — это признать, что рассматриваемый многочлен соответствует одному из трех конкретных шаблонов.Вам следует запомнить каждую из этих формул, чтобы сразу их заметить:

• Разница полных квадратов: x ² — a ² = ( x + a ) ( x — a )

• Разница идеальных кубов: a ³ — b ³ = ( a xs — b ) ( a ² + ab + b ² )

• Сумма идеальных кубов: a ³ + b ³ = ( a + b ) ( a ² — ab + b ² )

Пример 4: Полностью разложите следующие выражения на множители.

27 x ³ + 8

Обратите внимание, что 27 x ³ и 8 являются идеальными кубами, поэтому примените формулу суммы идеальных кубов:

20 x ² -405

Похоже, что это не соответствует ни одному из шаблонов, но для начала вы можете вычесть наибольший общий множитель 5:

Теперь более ясно, что (4 x ² — 81) является разностью полных квадратов, поскольку (2 x ) ² = 4 x ² и 9 ² = 81:

.