Что такое факторинг: простое и подробное объяснение, схема
Финансирование бизнеса » Услуги факторинга »
Факторинг представляет собой комплекс услуг, важнейшим звеном которого является уступка (продажа) дебиторской задолженности компании.
Факторинг простыми словами
Разберем приведенное выше определение подробнее и объясним его простыми доступными словами. Сущность факторинга очень проста, если отбросить специфические термины, разобраться в нем не составляет труда.
Долги одних компаний перед другими — это нормальное и широко распространенное явление. Именно долги в пользу конкретной фирмы называются ее дебиторской задолженностью. Как она возникает?
Например, оптовый продавец может отгрузить покупателю партию товара, а покупаетель рассчитывается с ним не сразу, а через неделю (по тем или иным причинам). Или: консалтинговая фирма провела анализ бизнеса другой организации, представила свои рекомендации, полностью выполнив условия договора.
Очевидно, что проволочки в оплате серьезно мешают бизнесу, снижая его устойчивость и способность к развитию. Возращаясь к самому простому примеру — торговле — пока покупатель не оплатил выставленный оптовиком счет, продавец не может приобрести новую партию товара для обслуживания других контрагентов.
Сущность факторинга как раз и заключается в ликвидации этих проволочек. Третье лицо (банк, специализированная факторинговая компания) выкупает обязательства покупателя, предоставляя продавцу «живые» деньги сразу после продажи товара. Разумеется, это делается не бесплатно — однако возможность бесперебойного функционирования бизнеса обычно позволяет легко «отбить» комиссию фактора.
Механизм факторинга
Механизм достаточно прост, сложности в понимании возникают в связи с необходимостью хорошо понимать роли участников сделки.
Их трое.
| Кредитор | Дебитор | Фактор | |
| Роль | Поставщик товаров или услуг | Покупатель, клиент кредитора | Банк или специализированная компания |
| Выгода от сделки | Бесперебойный бизнес, привлекательность товара для покупателя за счет отсрочки, грамотное управление задолженностью | Получение отсрочки платежа | Комиссия за предоставленные услуги |
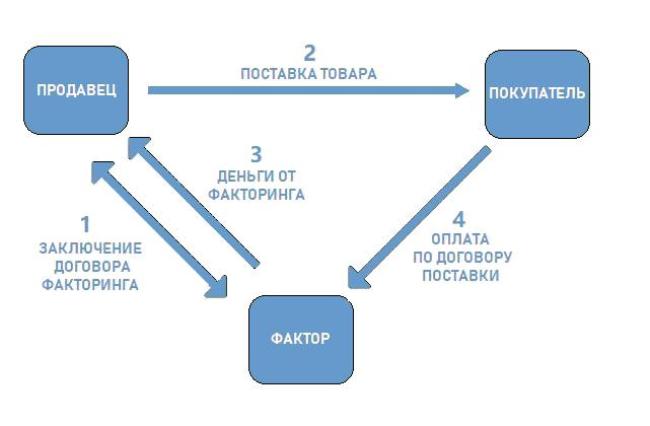
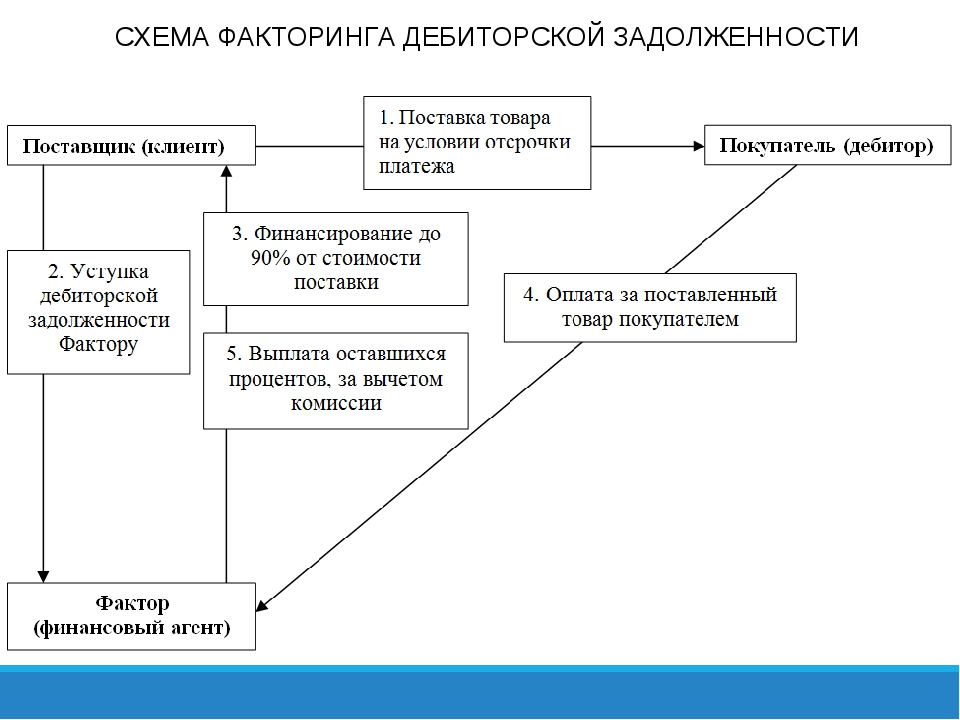
Вот обычные этапы процесса.
- Клиент факторинговой компании оказывает услуги или предоставляет покупателю товары и услуги с отсрочкой платежа.
- Клиент (продавец) передает фактору документы, подтверждающие факт появления дебиторской задолженности.
- Фактор покрывает большую часть задолженности (вплоть до 95%).
- Дебитор проводит оплату за товар или услуги.
- Кредитор и фактор проводят окончательные расчеты между собой: банк получает обратно свои деньги с дополнительной комиссией за услуги, продавец получает остаток полагающихся ему средств (5 — 30%).
Для окончательной ясности — ознакомьтесь со схемами.
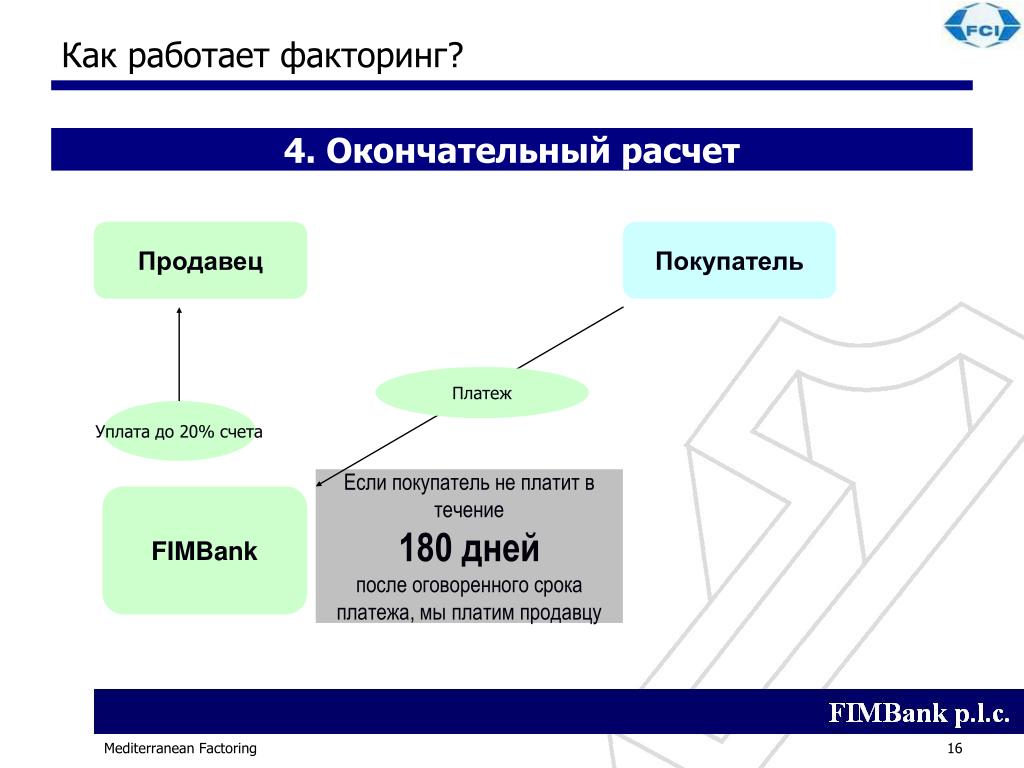
Схема факторинга
Это наиболее простой вариант — закрытый тип. Фактор проводит расчеты только с кредитором.
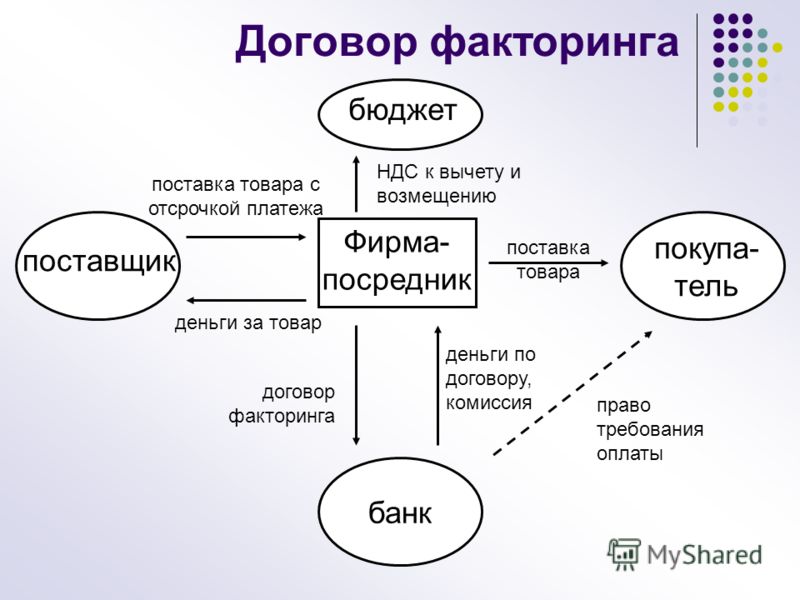
В более сложном варианте — открытом — отношения есть между всеми тремя участниками. Покупатель рассчитывается уже с банком — то есть задолженность полностью устуается фактору.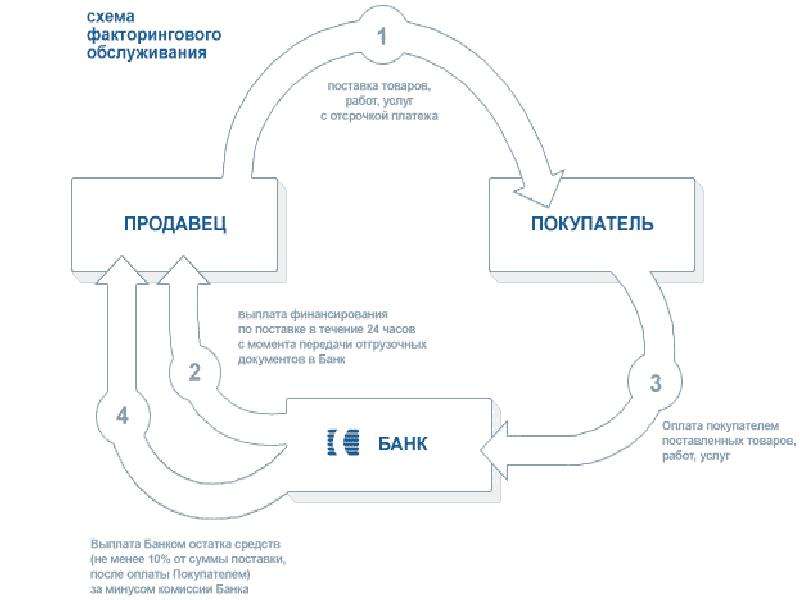
Остальные этапы аналогичны первой схеме. Разумеется, различия в документообороте при этом достаточно существенны.
Что такое факторинг простыми словами
Банк НФК (АО) Контакты:Адрес: ул. Кожевническая, д. 14 115114 Москва, Телефон:(495) 787-53-37, Телефон:(495) 995-21-31, Электронная почта: [email protected]
Адрес2: ул. Рокоссовского, д. 62, БЦ «ВолгоградСИТИ», оф. 15-21 400050 г. Волгоград, Телефон:(8442) 43-44-00, Электронная почта: [email protected]
Адрес3:
ул. Свободы, д. 73, офис 311
394018
Россия, г. Воронеж,
Телефон:(473) 228-19-78, 228-19-79,
Электронная почта: [email protected]
Свободы, д. 73, офис 311
394018
Россия, г. Воронеж,
Телефон:(473) 228-19-78, 228-19-79,
Электронная почта: [email protected]
Адрес4: ул. Хохрякова, 10, оф. 504-505 620014 Свердловская область, г. Екатеринбург, Телефон:(343) 310-14-55, Электронная почта: [email protected]
Адрес5: ул. Рабочая, д. 2а, офис 29А (3952) 486 331 г. Иркутск, Телефон:(3952) 486 331, Электронная почта: [email protected]
Адрес6:
ул. Декабристов, 85б, офис 409, 410
420034
г.
Адрес7: Ленинский пр., д. 30, офис 508 236006 г. Калининград, Телефон:(4012) 53-53-87, Электронная почта: [email protected]
Адрес8: ул. Красная д. 152 г. Краснодар, Телефон:(861) 226-42-52, 226-45-54, Электронная почта: [email protected]
Адрес9:
ул. Алексеева, д. 49, офис 6-14.
660077
г. Красноярск,
Телефон:(391) 200-28-20,
Электронная почта: kra_oa@factoring. ru
ru
Адрес10: ул. Нижегородская, 24 603000 г. Нижний Новгород, Телефон:(831) 288-02-89, Электронная почта: [email protected]
Адрес11: ул. Ленина, 52, офис 505 630004 г. Новосибирск, Телефон:(383) 212-06-18, 212-06-19, Электронная почта: [email protected]
Адрес12: ул. Николая Островского, 59/1 614007 г. Пермь, Телефон:(342) 211-50-28, Электронная почта: [email protected]
Адрес13:
ул. Красноармейская, д. 200, 8 этаж, оф. 803
344000
г. Ростов-на-Дону,
Телефон:(863) 263-88-30,
Электронная почта: [email protected]
Красноармейская, д. 200, 8 этаж, оф. 803
344000
г. Ростов-на-Дону,
Телефон:(863) 263-88-30,
Электронная почта: [email protected]
Адрес14: пр.К.Маркса, д.201 «Б» (бизнес-крепость «Башня») 443080 г. Самара, Телефон:(846)993-61-62, 993-61- 64, 993-61-63, Электронная почта: [email protected]
Адрес15: ул. Восстания, 18, офисы 405-407 191014 Санкт-Петербург, Телефон:(812) 644-40-71, Электронная почта: [email protected]
Адрес16:
ул.
Адрес17: ул. Крупской, д. 9, офис 727, 728, 729 450000 Республика Башкортостан, г. Уфа, Телефон:(347) 273-50-78, Электронная почта: [email protected]
Адрес18: ул. К. Маркса, д.38, офис 319 454091 г. Челябинск, Телефон:(351) 239-93-90, 239-93-91, 239-93-92, Электронная почта: [email protected]
Адрес19:
ул. Республиканская, д.3, корпус 1, офис 404
150003
г. Ярославль,
Телефон:(4852) 58-11-88,
Электронная почта: [email protected]
Республиканская, д.3, корпус 1, офис 404
150003
г. Ярославль,
Телефон:(4852) 58-11-88,
Электронная почта: [email protected]
|
Факторинг по алгебре
Факторы
У чисел есть множители:
И выражения (например, x 2 + 4x + 3 ) также имеют множители:
Факторинг
Факторинг (в Великобритании называется « Факторинг ») — это процесс нахождения факторов :
Факторинг: поиск того, что нужно умножить, чтобы получить выражение.
Это похоже на «разбиение» выражения на умножение более простых выражений.
Пример: множитель 2y + 6
У 2y и 6 есть общий множитель 2:
Таким образом, мы можем разложить все выражение на:
2у + 6 = 2 (у + 3)
Таким образом, 2y + 6 было «учтено» в 2 и y + 3
Факторинг также противоположен расширению:
Общий коэффициент
В предыдущем примере мы видели, что 2y и 6 имеют общий множитель 2
Но для правильного выполнения работы нам нужен наивысший общий множитель , включая любые переменные
Пример: коэффициент 3y
2 + 12y Во-первых, 3 и 12 имеют общий делитель 3.
Итак, мы могли бы иметь:
3 года 2 + 12 лет = 3 (год 2 + 4 года)
Но мы можем сделать лучше!
3y 2 и 12y также разделяют переменную y.
Вместе, что составляет 3 года:
- 3y 2 — 3y × y
- 12y — 3y × 4
Таким образом, мы можем разложить все выражение на:
3 года 2 + 12 лет = 3 года (y + 4)
Чек: 3y (y + 4) = 3y × y + 3y × 4 = 3y 2 + 12y
Более сложный факторинг
Факторинг может быть трудным!
До сих пор примеры были простыми, но факторизация может оказаться очень сложной.
Потому что мы должны изобразить то, что мы умножили на , чтобы получить данное нам выражение!
Это все равно, что пытаться найти, какие ингредиенты
пошли на торт, чтобы сделать его таким восхитительным.
Это может быть сложно понять!
Опыт помогает
Чем больше опыта, тем проще факторинг.
Пример: Фактор
4x 2 — 9Хммм … похоже, нет общих факторов.
Но знание специальных биномиальных произведений дает нам ключ к разгадке, который называется «разница квадратов». :
Потому что 4x 2 равно (2x) 2 , а 9 равно (3) 2 ,
Итак имеем:
4x 2 — 9 = (2x) 2 — (3) 2
А это можно получить по формуле разности квадратов:
(a + b) (a − b) = a 2 — b 2
Где a — 2x, а b — 3.
Итак, давайте попробуем это сделать:
(2x + 3) (2x − 3) = (2x) 2 — (3) 2 = 4x 2 — 9
Да!
Таким образом, множители 4x 2 — 9 равны (2x + 3) и (2x − 3) :
Ответ: 4x 2 -9 = (2x + 3) (2x − 3)
Как можно этому научиться? Получив много практики и зная «Самобытность»!
Помните эти личности
Вот список общих «Идентификаций» (включая «разность квадратов» , использованную выше).
Об этом стоит помнить, так как они могут облегчить факторинг.
| а 2 — б 2 | = | (а + б) (а-б) |
| a 2 + 2ab + b 2 | = | (а + б) (а + б) |
| a 2 — 2ab + b 2 | = | (а-б) (а-б) |
| a 3 + b 3 | = | (a + b) (a 2 −ab + b 2 ) |
| a 3 — b 3 | = | (a − b) (a 2 + ab + b 2 ) |
| a 3 + 3a 2 b + 3ab 2 + b 3 | = | (а + б) 3 |
| a 3 −3a 2 b + 3ab 2 −b 3 | = | (а-б) 3 |
Подобных гораздо больше, но это самые полезные.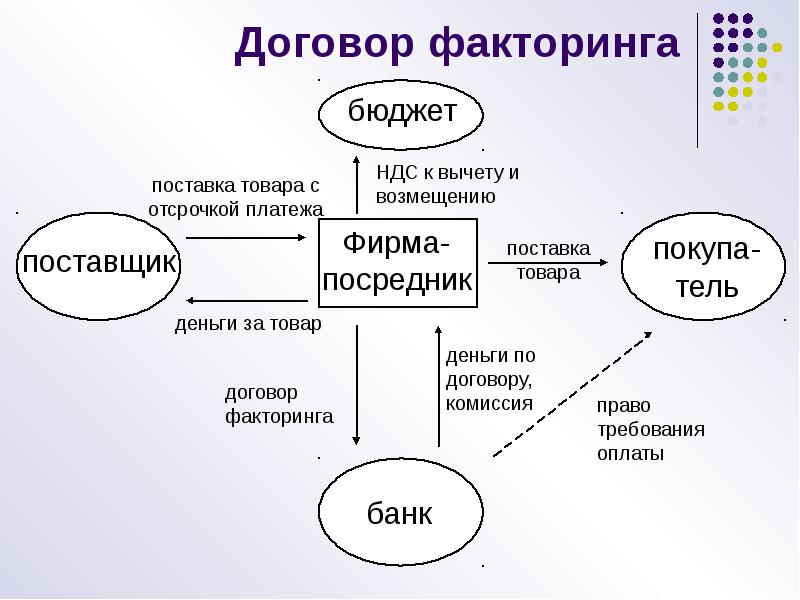
Совет
Факторизованная форма обычно лучше всего.
При попытке факторизации выполните следующие действия:
- «Вынести за скобки» любые общие термины
- Посмотрите, подходит ли он какой-либо из идентификационных данных, плюс еще какие-то, которые вы, возможно, знаете
- Продолжайте, пока вы больше не сможете множить
Существуют также системы компьютерной алгебры (называемые «CAS»), такие как Axiom, Derive, Macsyma, Maple, Mathematica, MuPAD, Reduce и многие другие, которые хорошо справляются с факторингом.
Другие примеры
Опыт действительно помогает, поэтому вот еще несколько примеров, которые помогут вам на этом пути:
Пример: w
4 — 16Показатель степени 4? Может быть, мы могли бы попробовать показатель степени 2:
w 4 — 16 = (w 2 ) 2 — 4 2
Да, это разница квадратов
w 4 — 16 = (w 2 + 4) (w 2 — 4)
И «(w 2 — 4)» — еще одно отличие квадратов
w 4 -16 = (w 2 + 4) (w + 2) (w -2)
Это все, что я могу (если я не использую мнимые числа)
Пример: 3u
4 — 24uv 3Удалить общий множитель «3u»:
3u 4 — 24uv 3 = 3u (u 3 — 8v 3 )
Тогда разница кубиков:
3u 4 — 24uv 3 = 3u (u 3 — (2v) 3 )
= 3u (u − 2v) (u 2 + 2uv + 4v 2 )
Это все, что я могу.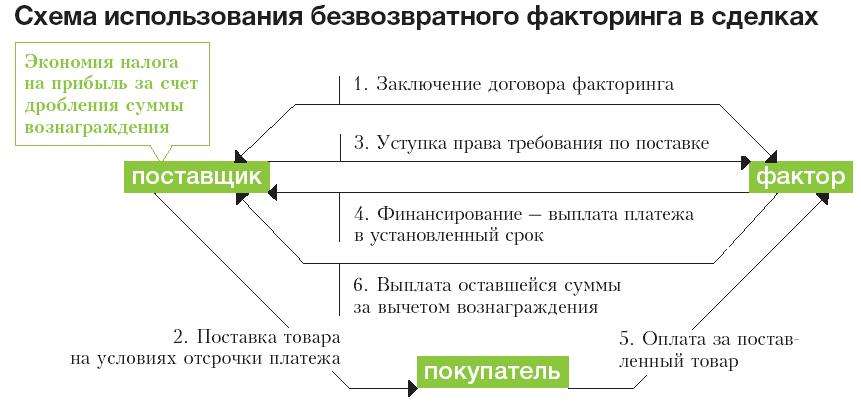
Пример: z
3 — z 2 — 9z + 9Попробуйте разложить на множители первые два и вторые два по отдельности:
z 2 (z − 1) — 9 (z − 1)
Вау, (z-1) есть на обоих, так что давайте воспользуемся этим:
(z 2 −9) (z − 1)
А z 2 −9 — разность квадратов
(г-3) (г + 3) (г-1)
Это все, что я могу.
А теперь побольше опыта:
Графические квадратные уравнения с использованием факторинга
Квадратное уравнение это многочлен уравнение степень 2 .Стандартная форма квадратного уравнения:
0 знак равно а Икс 2 + б Икс + c
куда
а
,
б
и
c
все реальные числа и
а
≠
0
.
Если мы заменим 0 с у , то получаем квадратичная функция
у знак равно а Икс 2 + б Икс + c
чей график будет парабола .
Точки пересечения графика
Икс
-оси будут решениями уравнения,
а
Икс
2
+
б
Икс
+
c
знак равно
0
. То есть, если многочлен
а
Икс
2
+
б
Икс
+
c
может быть учтен на
(
Икс
—
п
)
(
Икс
—
q
)
, мы знаем по
свойство нулевого продукта
что если
(
Икс
—
п
)
(
Икс
—
q
)
знак равно
0
, или
(
Икс
—
п
)
знак равно
0
или
(
Икс
—
q
)
знак равно
0
. Затем
п
и
q
являются решениями уравнения
а
Икс
2
+
б
Икс
+
c
знак равно
0
и поэтому
Икс
-перехваты квадратного уравнения.
Затем
п
и
q
являются решениями уравнения
а
Икс
2
+
б
Икс
+
c
знак равно
0
и поэтому
Икс
-перехваты квадратного уравнения.
Поскольку Икс -координата вершина параболы это точно середина Икс -перехватывает , то Икс -координата вершины будет п + q 2 .
Вы можете использовать Икс -координата вершины для нахождения у -координат.
Теперь у вас есть вершина и 2 другие точки параболы (а именно, Икс -перехватывает). Вы можете использовать эти три точки для построения графика.
Пример 1:
Постройте график функции
у
знак равно
Икс
2
—
8
Икс
+
12
с использованием факторинга.
Сравните уравнение со стандартной формой, у знак равно а Икс 2 + б Икс + c . Поскольку значение а положительный, парабола открывается.
Разложите на множители трехчлен, Икс 2 — 8 Икс + 12 . Идентифицировать 2 числа, сумма которых — 8 и продукт 12 .Цифры — 2 и — 6 . Это, Икс 2 — 8 Икс + 12 знак равно ( Икс — 2 ) ( Икс — 6 ) .
Икс 2 — 8 Икс + 12 знак равно 0 ⇒ ( Икс — 2 ) ( Икс — 6 ) знак равно 0
Итак, по свойству нулевого продукта либо
(
Икс
—
2
)
знак равно
0
или
(
Икс
—
6
)
знак равно
0
. Тогда корни уравнения равны
2
и
6
.
Тогда корни уравнения равны
2
и
6
.
Следовательно Икс -перехваты функции 6 и 2 .
В Икс -координата вершины — это середина х-точек пересечения. Итак, вот Икс -координата вершины будет 2 + 6 2 знак равно 4 .
Заменять Икс знак равно 4 в уравнении у знак равно Икс 2 — 8 Икс + 12 найти у -координата вершины.
у знак равно ( 4 ) 2 — 8 ( 4 ) + 12 знак равно 16 — 32 + 12 знак равно — 4
То есть координаты вершины равны
(
4
,
—
4
)
.
Теперь у нас 3 очка ( 4 , — 4 ) , ( 2 , 0 ) и ( 6 , 0 ) которые находятся на параболе. Нанесите точки. Соедините их плавной кривой и продолжите параболу.
Пример 2:
Постройте график функции у знак равно — Икс 2 — 2 Икс + 8 с использованием факторинга.
Сравните уравнение со стандартной формой, у знак равно а Икс 2 + б Икс + c . Поскольку значение а положительный, парабола открывается.
Разложите на множители трехчлен,
—
Икс
2
—
2
Икс
+
8
.
Во-первых, фактор вне — 1 .
— Икс 2 — 2 Икс + 8 знак равно — 1 ( Икс 2 + 2 Икс — 8 )
Разложите выражение на множители в скобках. Идентифицировать 2 числа, сумма которых 2 и продукт — 8 .Цифры 4 и — 2 . Это, Икс 2 + 2 Икс — 8 знак равно ( Икс + 4 ) ( Икс — 2 ) .
Тогда данная функция принимает вид
у
знак равно
—
(
Икс
+
4
)
(
Икс
—
2
)
.
Так, у знак равно 0 следует из свойства нулевого продукта, Икс + 4 знак равно 0 или Икс — 2 знак равно 0 .
Следовательно Икс -перехваты графика — 4 и 2 .
В Икс -координата вершины параболы — середина Икс -перехватывает.Итак, вот Икс -координата вершины будет — 4 + 2 2 знак равно — 1 .
Заменять
Икс
знак равно
—
1
в уравнении
у
знак равно
—
Икс
2
—
2
Икс
+
8
найти
у
-координата вершины.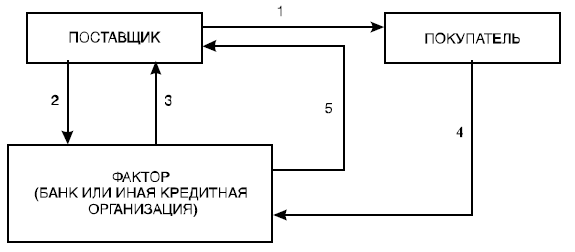
у знак равно — ( — 1 ) 2 — 2 ( — 1 ) + 8 знак равно — 1 + 2 + 8 знак равно 9
Итак, координаты вершины равны ( — 1 , 9 ) .
Теперь у нас есть
3
точки
(
—
1
,
9
)
,
(
—
4
,
0
)
и
(
2
,
0
)
которые находятся на параболе. Нанесите точки. Соедините их плавной кривой и продолжите параболу.
Нанесите точки. Соедините их плавной кривой и продолжите параболу.
Триномиальное разложение на множители: квадратный метод — ChiliMath
Факторинг с использованием метода «ящика» или «сетки» является отличной альтернативой факторингу трехчлена методом группирования, когда ведущий коэффициент a не равен 1 или -1.2} + bx + c должно быть 1 .
Шаги по разложению тринома на множители с использованием «квадратного» метода
Шаг 1 : Умножьте старший коэффициент и постоянный член (число без переменной).
Шаг 2 : Найдите два числа , такие, что произведение равно a · c , а сумма равна среднему коэффициенту b . Пусть « n » и « m » будут двумя числами, удовлетворяющими двум условиям.
Шаг 3 : Создайте сетку 2 × 2 и поместите следующие члены в правые поля:
- Поместите первый член в верхнее левое поле.

- Поместите постоянный член в нижнее правое поле.
- Поместите числа, найденные на шаге 2, в оставшиеся пустые поля. На этот раз неважно, где вы их разместите. Убедитесь, что вы добавили переменную x к каждому числу.
Шаг 4 : Найдите наибольший общий делитель в каждой строке и столбце.2} — 5x — 4 методом «коробки».
Начните с умножения ведущего коэффициента и постоянного члена.
\ влево (6 \ вправо) \ влево ({- 4} \ вправо) = — 24
Найдите пару факторов –24, так что сумма равна среднему коэффициенту, равному –5. Вы можете методом проб и ошибок выяснить это. Если вы все сделали правильно, у вас должны быть два числа −8 и 3, потому что
(–8) (3) = –24
(–8) + (3) = –5
Далее мы собираемся заполнить поле.2} — 18x + 9 методом «коробки».
Произведение главного коэффициента и постоянного члена равно (5) (9) = 45. Можете ли вы найти два числа, произведение которых равно 45, а сумма будет средним коэффициентом, равным −18?
Если задуматься, у двух чисел должны быть одинаковые знаки.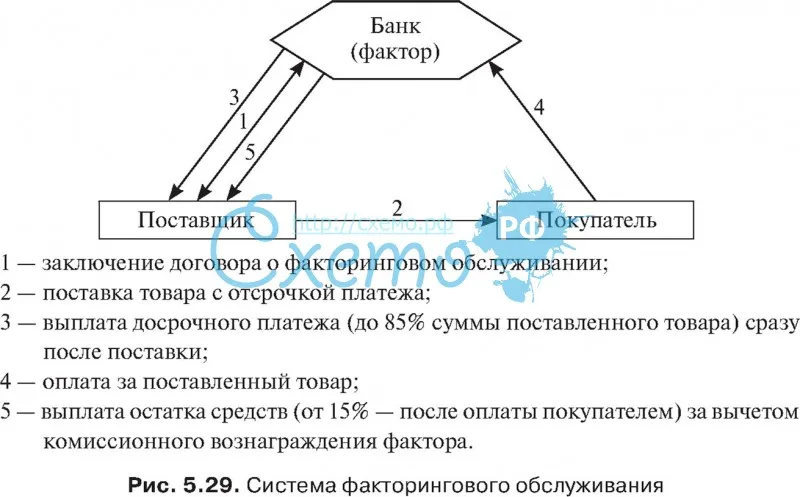 Это означает, что они должны быть как положительными, так и отрицательными. Если сложить два положительных числа, сумма будет положительной. Нам не нужен этот вариант, поскольку мы хотим, чтобы сумма была отрицательной.
Это означает, что они должны быть как положительными, так и отрицательными. Если сложить два положительных числа, сумма будет положительной. Нам не нужен этот вариант, поскольку мы хотим, чтобы сумма была отрицательной.
Это оставляет нам второй вариант: оба числа должны быть отрицательными.После проб и ошибок числа, которые могут удовлетворять двум условиям, равны −3 и −15. Так как,
\ влево ({- 3} \ вправо) \ влево ({- 15} \ вправо) = 45
\ left ({- 3} \ right) + \ left ({- 15} \ right) = — 18
Вот наша коробка с терминами в нужных местах.
Определите наибольший общий множитель (GCF) каждой строки и столбца. Не забудьте поставить знак ближайшего термина в рамке, которая находится либо справа от него, либо под ним.
Коэффициенты берутся по краям сетки.2} — 18x + 9 = \ влево ({5x — 3} \ вправо) \ влево ({x — 3} \ вправо)
Возможно, вас заинтересует:
Трехчлен разложения на множители, где a = 1
Трехчлен разложения на множители, где a> 1
Триномиальное разложение на множители — Метод и примеры
Владение алгеброй — ключевой инструмент в понимании и усвоении математики.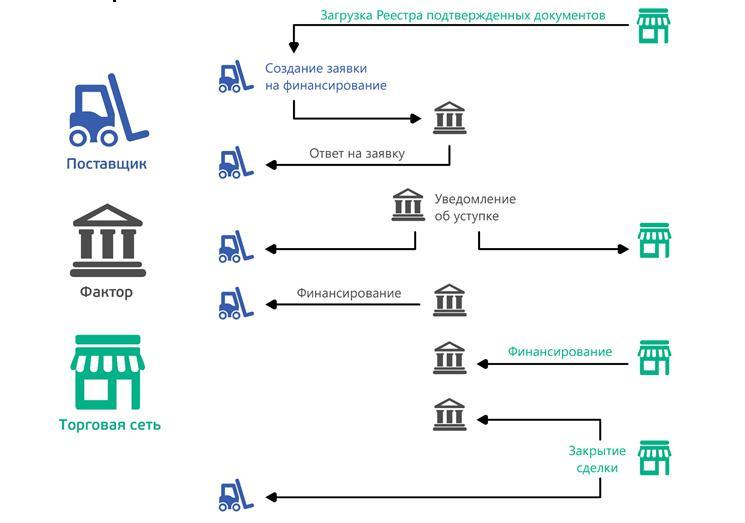 Для тех, кто стремится повысить свой уровень в изучении алгебры, факторинг является фундаментальным навыком , необходимым для решения сложных задач, связанных с многочленами.
Для тех, кто стремится повысить свой уровень в изучении алгебры, факторинг является фундаментальным навыком , необходимым для решения сложных задач, связанных с многочленами.
Факторинг используется на каждом уровне алгебры для решения многочленов, построения графиков функций и упрощения сложных выражений.
Как правило, факторизация — это операция, обратная раскрытию выражения.
Например, 3 (x — 2) является факторизованной формой 3x — 6, а (x — 1) (x + 6) является факторизованной формой x 2 + 5x — 6. В то время как расширение сравнительно это простой процесс, факторинг — немного сложная задача, и поэтому студент должен практиковать различные типы факторизации, чтобы получить навыки их применения.
Если есть какой-либо урок алгебры, который вызывает недоумение у многих студентов, то это тема факторизации трехчленов.
Эта статья поможет вам шаг за шагом понять, как решать проблемы, связанные с факторингом трехчленов. Следовательно, иллюзия того, что эта тема является самой сложной, будет вашей историей прошлого.
Следовательно, иллюзия того, что эта тема является самой сложной, будет вашей историей прошлого.
Вы узнаете, как разложить на множители все виды трехчленов, в том числе те, у которых старший коэффициент равен 1, и те, у которых старший коэффициент не равен 1.
Прежде чем мы начнем, полезно вспомнить следующие термины:
Коэффициент — это число, которое делит другое данное число, не оставляя остатка . У каждого числа есть коэффициент, который меньше или равен самому числу.
Например, множители числа 12 сами по себе равны 1, 2, 3, 4, 6 и 12. Мы можем заключить, что все числа имеют множитель 1, и каждое число является множителем само по себе.
До изобретения электронных и графических калькуляторов факторизация была самым надежным методом нахождения корней полиномиальных уравнений .
Хотя квадратные уравнения давали решения, которые были более прямыми по сравнению со сложными уравнениями, они были ограничены только для
полиномов второй степени.
Факторинг позволяет нам переписать многочлен в более простые множители , и, приравняв эти множители к нулю, мы можем определить решения любого полиномиального уравнения.
Существует нескольких методов факторизации полиномов . В этой статье основное внимание будет уделено тому, как разложить на множители различные типы трехчленов, например трехчлены с ведущим коэффициентом, равным 1, и с ведущим коэффициентом, не равным 1.
Прежде чем мы начнем, мы должны ознакомиться со следующими условиями.
Общий множитель определяется как число, которое можно разделить на два или более разных числа, не оставляя остатка.
Например, общие множители чисел 60, 90 и 150 равны; 1, 2, 3,5, 6,10, 15 и 30.
- Наибольший общий коэффициент (GCF)
Наибольший общий делитель чисел — это наибольшее значение множителей данных чисел . Например, учитывая общие множители 60, 90 и 150: 1, 2, 3,5, 6,10, 15 и 30, поэтому наибольший общий множитель равен 30.
Например, учитывая общие множители 60, 90 и 150: 1, 2, 3,5, 6,10, 15 и 30, поэтому наибольший общий множитель равен 30.
GCF. для трехчлена — это наибольший одночлен, который делит каждый член трехчлена. Например, чтобы найти GCF выражения 6x 4 — 12x 3 + 4x 2 , мы применяем следующие шаги:
- Разбиваем каждый член трехчлена на простые множители.
(2 * 3 * x * x * x * x) — (2 * 2 * 3 * x * x * x) + (2 * 2 * x * x)
- Ищите факторы, которые появляются в каждом один термин выше.
Вы можете обвести или раскрасить множители следующим образом:
(2 * 3 * x * x * x * x) — (2 * 2 * 3 * x * x * x) + (2 * 2 * x * x )
Следовательно, GCF для 6x 4 — 12x 3 + 4x 2 равно 2x 2
Полином — это алгебраическое выражение, содержащее более двух членов, таких как переменные и числа , обычно объединены операциями сложения или вычитания.
Примеры многочленов: 2x + 3, 3xy — 4y, x² — 4x + 7 и 3x + 4xy — 5y.
Трехчлен — это алгебраическое уравнение, состоящее из трех членов и обычно имеющее форму ax 2 + bx + c = 0, где a, b и c — числовые коэффициенты. Число «a» называется старшим коэффициентом и не равно нулю (a 0).
Например, x² — 4x + 7 и 3x + 4xy — 5y являются примерами трехчленов. С другой стороны, бином — это алгебраическое выражение, состоящее из двух членов. Примеры биномиального выражения включают; x + 4, 5 — 2x, y + 2 и т. д.
Фактор трехчлена означает разложение уравнения на произведение двух или более биномов.Это означает, что мы перепишем трехчлен в виде (x + m) (x + n).
Ваша задача определить значение m и n. Другими словами, мы можем сказать, что факторизация трехчлена — это процесс, обратный методу фольги.
Как разложить на множители трехчлены со старшим коэффициентом 1
Давайте рассмотрим следующие шаги, чтобы разложить множители x 2 + 7x + 12:
- Сравнение x 2 + 7x + 12 со стандартной формой ax 2 + bx + c, получаем, a = 1, b = 7 и c = 12
- Найдите парные множители c, сумма которых равна b.Парный множитель 12 равен (1, 12), (2, 6) и (3, 4). Следовательно, подходящей парой является 3 и 4.
- В отдельных скобках добавьте каждое число пары к x, чтобы получить (x + 3) и (x + 4).
- Запишите два бинома рядом, чтобы получить результат с разложением;
(х + 3) (х + 4).
Как разложить на множители трехчлены с помощью GCF?
Чтобы разложить на множители трехчлен с ведущим коэффициентом, не равным 1, мы применяем концепцию наибольшего общего множителя (GCF) как , показанную на шагах ниже:
- Если трехчлен находится в неправильном порядке, перепишите это в порядке убывания, от наибольшей к наименьшей степени.
- Вынесите GCF за скобки и не забудьте включить его в свой окончательный ответ.
- Найдите произведение старшего коэффициента «a» и константы «c».
- Перечислите все факторы произведения a и c из шага 3 выше. Определите комбинацию, которая в сумме даст число рядом с x.
- Перепишите исходное уравнение, заменив термин «bx» на коэффициенты, выбранные на шаге 4.
- Разложите уравнение на множители, сгруппировав его.
Подводя итог этому уроку, мы можем разложить на множители трехчлен вида ax 2 + bx + c, применив любую из этих пяти формул:
- a 2 + 2ab + b 2 = (a + б) 2 = (a + b) (a + b)
- a 2 — 2ab + b 2 = (a — b) 2 = (a — b) (a — b)
- a 2 — b 2 = (a + b) (a — b)
- a 3 + b 3 = (a + b) (a 2 — ab + b 2 )
- a 3 — b 3 = (a — b) (a 2 + ab + b 2 )
Давайте теперь разложим на множители пару примеров трехчленных уравнений.
Пример 1
Фактор 6x 2 + x — 2
Решение
GCF = 1, поэтому это бесполезно.
Умножьте старший коэффициент a на константу c.
⟹ 6 * -2 = -12
Перечислите все множители 12 и определите пару, которая имеет произведение -12 и сумму 1.
⟹ — 3 * 4
⟹ -3 + 4 = 1
Теперь перепишите исходное уравнение, заменив член «bx» выбранными множителями
⟹ 6x 2 — 3x + 4x — 2
Разложите выражение на множители путем группировки.
⟹ 3x (2x — 1) + 2 (2x — 1)
⟹ (3x + 2) (2x — 1)
Пример 2
Фактор 2x 2 — 5x — 12.
Решение
2x 2 — 5x — 12
= 2x 2 + 3x — 8x — 12
= x (2x + 3) — 4 (2x + 3)
= (2x + 3 ) (x — 4)
Пример 3
Фактор 6x 2 -4x -16
Решение
GCF для 6, 4 и 16 равно 2.
Вынести за скобки ЗКФ.
6x 2 — 4x — 16 ⟹ 2 (3x 2 — 2x — 8)
Умножьте старший коэффициент «a» на константу «c».
⟹ 6 * -8 = — 24
Определите парные множители 24 и сумму -2. В данном случае факторы 4 и -6.
⟹ 4 + -6 = -2
Перепишите уравнение, заменив член «bx» выбранными множителями.
2 (3x 2 — 2x — 8) ⟹ 2 (3x 2 + 4x — 6x — 8)
Сгруппируйте множители и не забудьте включить GCF в свой окончательный ответ.
⟹ 2 [x (3x + 4) — 2 (3x + 4)]
⟹ 2 [(x — 2) (3x + 4)]
Пример 4
Фактор 3x 3 — 3х 2 — 90х.
Решение
Поскольку GCF = 3x, множите его;
3x 3 — 3x 2 — 90x ⟹3x (x 2 — x — 30)
Найдите пару множителей, произведение которых равно −30, а сумма равна −1.
⟹- 6 * 5 = -30
⟹ −6 + 5 = -1
Перепишите уравнение, заменив член «bx» на выбранные множители.
⟹ 3x [(x 2 — 6x) + (5x — 30)]
Разложите уравнение на множители;
⟹ 3x [(x (x — 6) + 5 (x — 6)]
= 3x (x — 6) (x + 5)
Пример 5
Фактор 6z 2 + 11z + 4.
Решение
6z 2 + 11z + 4 ⟹ 6 z 2 + 3 z + 8 z + 4
⟹ (6 z 2 + 3 z ) + (8 z + 4)
⟹ 3z (2z + 1) + 4 (2z + 1)
= (2 z + 1) (3 z + 4)
Практические вопросыРазложите на множители каждое из следующих трехчленов.
- x 2 + 5x + 6
- x 2 + 10x + 24
- x 2 + 12x + 27
- x 2 + 15x + 5
- x 2 + 19x + 60
- x 2 + 13x + 40
- x 2 — 10x + 24
- x 2 — 23x + 42
- x 2 — 17x + 16
- x 2 — 21x + 90
- x 2 — 22x + 117
- x 2 — 9x + 20
- x 2 + x — 132
- x 2 + 5x — 104
- y 2 + 7y — 144
Ответы
- (x + 3) (x + 2)
- (x + 6) (x + 4)
- (x + 9) (x + 3)
- (x + 8 ) (x + 7)
- (x + 15) (x + 4)
- (x + 8) (x + 5)
- (x — 6) (x — 4)
- (x — 21) ( x — 2)
- (x — 16) (x — 1)
- (x — 15) (x — 6)
- (x — 13) (x — 9)
- (x — 5) (x — 4)
- (x + 12) (x — 11)
- (x + 13) (x — 8)
- (y + 16) (y — 9)
Алгебра — факторинг многочленов
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметкиПохоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 1-5: Факторинг многочленов
Из всех тем, затронутых в этой главе, разложение многочленов, вероятно, является наиболее важной темой.В последующих главах есть много разделов, в которых первым шагом будет факторизация многочлена. Итак, если вы не можете разложить многочлен на множители, вы не сможете даже начать задачу, не говоря уже о ее завершении.
Давайте начнем с того, что немного поговорим о том, что такое факторинг. Факторинг — это процесс, с помощью которого мы определяем, что мы умножили, чтобы получить заданное количество. Мы все время делаем это с числами. Например, вот несколько способов множителя 12.
\ [\ begin {align *} 12 & = \ left (2 \ right) \ left (6 \ right) & \ hspace {0.5 дюймов} 12 & = \ left (3 \ right) \ left (4 \ right) & \ hspace {0,25 дюйма} 12 & = \ left (2 \ right) \ left (2 \ right) \ left (3 \ right) \ hspace {0,25 дюйма} \\ 12 & = \ left ({\ frac {1}} \ right) \ left ({24} \ right) & \ hspace {0,5 дюйма} 12 & = \ left ({ — 2} \ right) \ left ({- 6} \ right) & \ hspace {0,5 дюйма} 12 & = \ left ({- 2} \ right) \ left (2 \ right) \ left ({- 3} \ вправо) \ end {align *} \]Есть еще много возможных способов множителя 12, но они репрезентативны для многих из них.
Общий метод разложения чисел на множители состоит в том, чтобы полностью разложить числа на положительные простые множители. Простое число — это число, единственные положительные делители которого равны 1 и самому себе. Например, 2, 3, 5 и 7 являются примерами простых чисел. Примеры непростых чисел: 4, 6 и 12, чтобы выбрать несколько.
Если мы полностью разложим число на положительные простые множители, будет только один способ сделать это. Это причина такого факторинга.Для нашего примера выше с 12 полная факторизация:
\ [12 = \ влево (2 \ вправо) \ влево (2 \ вправо) \ влево (3 \ вправо) \] Факторинг многочленов выполняется примерно таким же образом. Мы определяем все члены, которые были перемножены, чтобы получить заданный многочлен. Затем мы пытаемся разложить на множители каждый из терминов, найденных на первом этапе. Это продолжается до тех пор, пока мы больше не сможем принимать во внимание факторы. Когда мы больше не сможем разложить на множители, мы скажем, что полином полностью разложен на множители.2} + 4} \ right) \ left ({x + 2} \ right) \ left ({x — 2} \ right) \] Цель этого раздела — познакомиться со многими методами разложения многочленов на множители. Первый метод разложения полиномов на множители — это разложение на множители наибольшего общего множителя . При факторинге в целом это также будет первое, что мы должны попробовать, поскольку это часто упрощает проблему. Чтобы использовать этот метод, все, что мы делаем, — это просматриваем все термины и определяем, есть ли фактор, общий для всех терминов.Если есть, мы вычленим его из полинома. Также обратите внимание, что в этом случае мы действительно используем только закон распределения в обратном порядке. Помните, что согласно закону о дистрибьюции Выделяя наибольший общий фактор, мы делаем это в обратном порядке. Мы замечаем, что в каждом члене есть \ (a \), и поэтому мы «факторизуем» его, используя закон распределения в обратном порядке: Давайте взглянем на несколько примеров.5} — 3x + 1} \ right) \] Обратите внимание на «+1», где 3 \ (x \) изначально было в последнем члене, поскольку последний член был термином, который мы вычленили, нам нужно было напомнить себе, что изначально там был термин. Для этого нам понадобится «+1», и обратите внимание, что это «+1» вместо «-1», потому что термин изначально был положительным. Если бы изначально это был отрицательный термин, нам пришлось бы использовать «-1». Одна из наиболее распространенных ошибок, связанных с этим типом задач факторинга, — это забыть об этой цифре.2} + 6 \) Показать решение У этого термина также есть «-» перед третьим членом, как мы видели в предыдущей части. Однако на этот раз перед четвертым членом стоит знак «+», в отличие от последней части. Мы по-прежнему будем вычеркивать «-» при группировании, чтобы убедиться, что мы не теряем его из виду. Когда мы выносим за скобки «-», обратите внимание, что нам нужно заменить «+» в четвертом члене на «-». Опять же, вы всегда можете проверить, что это было сделано правильно, умножив «-» на круглые скобки.3} — 2} \ right) \] Факторинг по группировке может быть приятным, но срабатывает не так уж часто. Обратите внимание, что, как мы видели в последних двух частях этого примера, если перед третьим членом стоит «-», мы часто также вычленяем его из третьего и четвертого терминов, когда мы их группируем. Во-первых, отметим, что квадратичный — это еще один термин, обозначающий многочлен второй степени. Итак, мы знаем, что наибольший показатель квадратичного многочлена будет равен 2.{2} \), и единственный способ добиться этого — это умножить \ (x \) на \ (x \). Следовательно, первым членом каждого множителя должен быть \ (x \). Чтобы закончить это, нам просто нужно определить два числа, которые должны стоять на пустых местах. Мы можем значительно сузить возможности. После умножения двух множителей эти два числа нужно будет умножить, чтобы получить -15. Другими словами, эти два числа должны быть множителями -15. Вот все возможные способы множителя -15, используя только целые числа. Теперь мы можем просто вставить их один за другим и умножать, пока не получим правильную пару. Однако есть еще одна хитрость, которую мы можем использовать здесь, чтобы помочь нам. Чтобы получить коэффициент при члене \ (x \), необходимо сложить правильную пару чисел.2} \) означает умножение 3 \ (x \) и \ (x \), это должны быть первые два члена. Однако найти числа для двух пробелов будет не так просто, как в предыдущих примерах. Нам нужно будет начать со всеми множителями -8. На данный момент единственный вариант — выбрать пару, подключить их и посмотреть, что произойдет, когда мы умножим члены. 2} + 2x — 8 \] Итак, мы получили.2} — 17x + 6 = \ left ({5x + \ underline {\, \, \, \,}} \ right) \ left ({x + \ underline {\, \, \, \,}} \ right ) \] Далее нам нужны все множители 6. Вот они. Не забывайте о негативных факторах. Часто именно они нам и нужны. Фактически, заметив, что коэффициент при \ (x \) отрицателен, мы можем быть уверены, что нам понадобится одна из двух пар отрицательных факторов, так как это будет единственный способ получить там отрицательный коэффициент.2} + 10x — 6 & = \ left ({2x + \ underline {\, \, \, \,}} \ right) \ left ({2x + \ underline {\, \, \, \,}} \ вправо) \ end {align *} \] Чтобы заполнить пробелы, нам понадобятся все множители -6. 2} + 10x — 6 = \ left ({2x — 1} \ right) \ left ({2x + 6} \ right) \] Также обратите внимание, что на этапе проб и ошибок мы должны убедиться и включить каждую пару в обе возможные формы и в оба возможных порядка, чтобы правильно определить, является ли это правильной парой факторов или нет.2} \] Это просто неверно для подавляющего большинства сумм квадратов, поэтому будьте осторожны, чтобы не совершить эту очень распространенную ошибку. Есть редкие случаи, когда это можно сделать, но ни один из этих особых случаев здесь не рассматривается. В целом не существует единого метода для этого. Однако есть некоторые, что мы можем сделать, поэтому давайте рассмотрим несколько примеров. Обратите внимание, что это преобразование в \ (u \) вначале может быть полезно в некоторых случаях, однако, как только вы к этому привыкнете, это обычно происходит в наших головах. Мы не сделали здесь много задач и не рассмотрели все возможности. Однако мы рассмотрели некоторые из наиболее распространенных приемов, с которыми мы можем столкнуться в других главах этой работы. Наибольший общий коэффициент
Разложение квадратичных многочленов на множители
Факторинговые многочлены со степенью больше 2
Иллюстративная математика Алгебра 2, Раздел 2.2-7х + 12 \). Обратите внимание, что 24 в правом нижнем углу — это именно то, что нам нужно, и именно поэтому мы узнаем, что \ ((x + 2) \) является множителем \ (p (x) \). На следующем уроке мы увидим, почему это произошло. Немного увеличив факторизацию, мы можем сказать, что \ (p (x) = (x + 2) (x-3) (x-4) \).
Что такое факторинг? определение, виды и процедура
Определение : Факторинг подразумевает финансовое соглашение между фактором и клиентом, при котором фирма (клиент) получает авансы в обмен на дебиторскую задолженность от финансового учреждения (фактора).Это метод финансирования, при котором имеется прямая продажа торговой задолженности фирмой третьей стороне, то есть фактору, по сниженным ценам .
Факторинг — это финансовая альтернатива в финансировании и управлении дебиторской задолженностью. В договоре факторинга указаны условия продажи.
Говоря более тонко, факторинг — это отношения между фактором и клиентом, при которых фактор покупает дебиторскую задолженность клиента и выплачивает до 80% (иногда 90%) суммы немедленно, в момент заключения договора.Фактор выплачивает клиенту сумму баланса, то есть 20% от суммы, которая включает финансовые и операционные расходы, когда клиент оплачивает обязательство.
Виды факторинга
- Факторинг с регрессом и без права регресса : В рамках этого типа соглашения финансовое учреждение может обратиться к фирме, когда долги не подлежат возмещению. Таким образом, фактор не принимает на себя кредитный риск, связанный с торговой задолженностью.
С другой стороны, при факторинге без права регресса фактор не может обратиться к фирме в случае, если долг окажется безнадежным.
- Раскрытый и нераскрытый факторинг : Факторинг, при котором наименование фактора указывается в счете-фактуре поставщиком товаров или услуг, который просит покупателя оплатить фактор, называется раскрытым факторингом.
И наоборот, форма факторинга, при которой название фактора не упоминается в счете, выставленном производителем. В таком случае фактор ведет книгу продаж клиента, и долг реализуется на имя фирмы. Однако контроль находится в руках фактора.
- Внутренний и экспортный факторинг : Когда три стороны факторинга, то есть клиент, клиент и фактор, проживают в одной стране, это называется внутренним факторингом.
Экспортный факторинг, иначе известный как трансграничный факторинг, включает четыре стороны, то есть экспортер (клиент), импортер (заказчик), фактор экспорта и фактор импорта. Это также называется двухфакторной системой.
- Факторинг с авансом и сроком погашения : В рамках предварительного факторинга фактор предоставляет клиенту аванс в счет непогашенной дебиторской задолженности.
В факторинге по срокам погашения факторинговое агентство не предоставляет фирме никаких авансовых выплат. Вместо этого банк получает сумму от клиента и выплачивает фирме либо в день получения суммы от клиентов, либо в дату гарантированного платежа.
В зависимости от типа факторинга, взыскание долга осуществляется фактором или клиентом, в зависимости от обстоятельств.
Процедура
Процесс факторинга- Заемная компания или клиент продает балансовую задолженность кредитной организации (фактору).
- Фактор приобретает дебиторскую задолженность и предоставляет деньги в счет дебиторской задолженности после вычета и удержания следующей суммы, то есть адекватной маржи, комиссии фактора и процентов по авансу
- Инкассо от клиента пересылается клиентом фактору, и таким образом выплачивается аванс.
- Прочие услуги также оказывает фактор, в который входит:
- Финансы
- Взыскание долгов
- Обслуживание долгов
- Защита кредитного риска
- Ведение книги дебиторов
- Сопровождение дебиторов
- Консультационные услуги
Фактор получает контроль над дебиторами клиента, которым товары продаются в кредит или предоставляется кредит, а также контролирует книгу продаж клиента.
 mkb.ru/
mkb.ru/ ru/Единственный комфортный способ избежать кассового разрыва и увеличить оборот. Факторингс особым отношением к нуждам малого и среднего …
ru/Единственный комфортный способ избежать кассового разрыва и увеличить оборот. Факторингс особым отношением к нуждам малого и среднего …