Доходность за вычетом инфляции. Считаем правильно реальную доходность
01 июн 2015 Сергей Кикевич Все авторы

В прошлой публикации Где интуиция не срабатывает: считаем доходность мы рассказывали об алгебраической и геометрической суммах. Речь шла о том, как правильно считать доходность.
Когда мы употребляем термин доходность, то в большинстве случаев имеется ввиду номинальная доходность, то есть без учета инфляции. Как правило, инвестора интересует реальная доходность с учетом влияния инфляции.
Как и в прошлой статье начнем с простого примера. Если доходность депозита составила 18% годовых, а инфляция за тот же период — 11%, какова итоговая доходность?
18% — 11% =?
Проверьте себя. Как бы вы посчитали результат?
Что случится, если вдруг инфляция в этот год взлетит до 118%?
18% — 118% = ?
Довольно часто в первом случае люди полагают, что Реальная доходность составила 7%:
18% — 11%=7%
Такое вычитание называется алгебраическим.
Работает ли алгебраическое вычитание во втором случае?
18% — 118%= -100%
Может ли реальная доходность достигать -100% после учета инфляции? Это значило бы, что покупательная сила денег стала равной нулю. А если инфляция составила бы 120%, мы потеряли бы больше денег, чем у нас было? Вряд ли такой метод вычитания может быть правильным …
Как и раньше, помогает геометрическая разница:
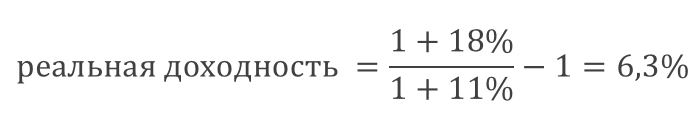
При расчете процентные соотношения переводятся в десятичные дроби, хотя в EXCEL можно этого не делать. EXCEL умеет сам переводить из дробей в проценты и наоборот (см. прилагаемый файл).
Если доходность составила R процентов, а инфляция равняется N, то реальная доходность вычисляется по формуле:
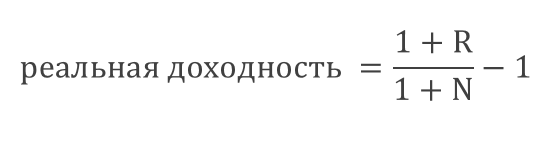
В примере, когда номинальная доходность составила 18% а инфляция – 11%, можно заметить, что результаты алгебраического и геометрического вычитания довольно близки. Ошибка составит лишь 0,69%.
Действительно, иногда полезно пользоваться алгебраической разницей для получения приближенных результатов. Ошибка будет незначительной в тех случаях, когда инфляция и доходность не слишком сильно отличаются.
Тем не менее, когда рассматриваются доходности за несколько периодов или когда разница между номинальной доходностью и инфляцией значительна, величина ошибки возрастает.

Понравилась статья?
Самое интересное и важное в нашей рассылке
Анонсы свежих статей Информация о вебинарах Советы экспертов
Нажимая на кнопку «Подписаться», я соглашаюсь с политикой конфиденциальности

rostsber.ru
Как рассчитать среднегодовую реальную доходность?
У некоторых читателей возник вопрос о том, как считать средне-годовую реальную доходность?
Решение довольно простое, но не всегда очевидное, особенно, в российской действительности.
Для расчета реальной доходности используется формула Фишера: Др=(1+Дн)/(1+И) – 1
где, Дн — номинальная доходность, И — инфляция, Др — реальная доходность
Упрощенную формулу Фишера в виде Др = Дн – И можно применять лишь в случаях маленьких значений Дн и И. Маленькими можно назвать значения в 1-5%. Для значений в 10% и выше упрощенная формула Фишера применяться не может, т.к. ведет к большим погрешностям.
Например,
Номинальная доходность за год Дн=6%
Инфляция за этот же период И=3%
Согласно формуле Фишера реальная доходность равна Др=2,91%, а с помощью упрощенной формулы Фишера равна Др=3,0%. Погрешность равна примерно 3%. Терпимо.
Теперь допустим, что:
Номинальная доходность за год Дн=15%
Инфляция за этот же период И=11%
Согласно формуле Фишера реальная доходность равна Др=3,6%, а с помощью упрощенной формулы Фишера получаем Др=4,0%. Погрешность в этом случае равна 11%. Это уже много.
Применим формулу Фишера для нескольких периодов.
1 год:
Х0 – начальная стоимость актива
Х1 – конечная стоимость актива
И1 – инфляция в первом году
Др1 – реальная доходность в первом году
Таким образом, стоимость актива (номинальная, т.е. наблюдаемая нами) равна:
Х1=Х0*(1+И1)*(1+Др1)
В конце второго года стоимость актива равна:
Х2=Х1*(1+И2)*(1+Др2)=Х0*(1+И1)*(1+Др1)*(1+И2)*(1+Др2)
В конце N-го года стоимость актива равна:
ХN=Х0*(1+И1)*(1+И2)*…*(1+ИN)*(1+Др1)*(1+Др2)*…*(1+ДрN)
Где:
(1+И1)*(1+И2)*…*(1+ИN)=(1+Исрг)N – формула средне-годовой инфляции за период (геометрическая средняя)
(1+Др1)*(1+Др2)*…*(1+ДрN)=(1+Дрсрг)N – формула средне-годовой реальной доходности за период (геометрическая средняя)
Таким образом, средне-годовая реальная доходность за период вычисляется по формуле:
Дрсрг = [(ХN/X0)*(1/(1+Исрг)N]1/N-1
или, заменив ХN/X0 на (1+Днсрг)N , получим формулу Фишера:
Дрсрг = [(1+Днсрг)N )/(1+Исрг)N]1/N-1
Вычислять среднегодовую доходность по формуле: Дрсрг = Днсрг – Исрг при больших значениях инфляции нельзя, т.к. очень велика погрешность.
dokmur.livejournal.com
зачем инвестору макроэкономика? Инфляция и процентные ставки
В соответствии с этой формулой уровень цен определяется по формуле: P=MV/Q
Количество денег в обращении (денежная масса) М =PQ/V
Исходя из данной формулы, Фишер делает вывод, что стоимость денег обратно пропорциональна их количеству. Формула Фишера MV = PQ позволяет объяснить явление инфляции с точки зрения нарушений в сфере бумажно-денежного обращения. Экономическая трактовка формулы М =PQ/V: чем больше созданный в стране национальный продукт, тем больше денег должно находиться в обращении. С увеличением физического количества товаров и цен этих товаров приходится наращивать денежную массу, и, наоборот, по мере уменьшения количества товаров и цен на них следует сужать денежную массу. В условиях инфляции масса денег в обращении оказывается чувствительной по отношению к уровню цен. Для нормального функционирования товарооборота и денежного обращения приходится увеличивать денежную массу в соответствии с ростом цен. Несоблюдение этого принципа ведет к сбоям в функционировании товарно-денежной системы, дефициту денег в обращении. Контроль со стороны государства за денежной массой необходим в целях воздействия на цены, производство, в целом на экономику.
Wikimedia Foundation . 2010 .
Смотреть что такое «Формула Фишера» в других словарях:
Устойчивое распределение в теории вероятностей это такое распределение, которое может быть получено как предел по распределению сумм независимых случайных величин. Содержание 1 Определение 2 Замечания 3 Свойства устойчивых распределений … Википедия
Точный тест Фишера тест статистической значимости, используемый в анализе таблиц сопряжённости признаков для выборок маленьких размеров. Назван именем своего изобретателя Р. Фишера. Относится к точным тестам значимости, поскольку не… … Википедия
Формула, задающая соотношение между изменением банковских процентных ставок и изменением спот курсов валют. Согласно международному эффекту Фишера разница в процентных ставках между двумя странами должна быть несмещенным предиктором будущего… … Финансовый словарь
РАСПРЕДЕЛЕНИЕ ФИШЕРА — – аналог нормального распределения на сфере. Статистика Р.Фишера широко применяется при обработке палеомагнитных данных. Проверка соответствия реальных распределений векторов Jn и ее компонент распределению Фишера помогает оценить… … Палеомагнитология, петромагнитология и геология. Словарь-справочник.
Асимптотическое разложение разности между соответствующими квантилями нормального распределения и какого либо близкого к нему распределения по степеням малого параметра; изучено Э. Корнишем и Р. Фишером . Если F(x, t) функция распределения,… … Математическая энциклопедия
Покупательная сила денег: ее определение и отношение к кредиту, проценту и кризисам (англ. The Purchasing Power of Money: Its determination and relation to credit, interest and crises, 1911) произведение американского экономиста И. Фишера.… … Википедия
Процентная ставка — (Interest rate) Процентная ставка это процент денежной прибыли, которую заемщик выплачивает кредитору за взятый в ссуду денежный капитал Определение процентной ставки, виды процентных ставок по кредитам, реальная и номинальная процентные… … Энциклопедия инвестора
Z-преобразование — Формула преобразования выборки величин г (коэффициент корреляции) с тем, чтобы приблизить их к нормальному распределению. Также называется Z преобразованием Фишера … Толковый словарь по психологии
Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случ
windows10official.ru
Инфляция и реальная ставка процента. Реальная доходность и формула Фишера. Финансовая математика
Существует два основных показателя (параметра), характеризующих инфляцию: темп инфляции и индекс инфляции. Ниже дадим определение и приведем формулы для расчета обоих показателей (параметров) инфляции.
Инфляция оценивается за некоторый период времени.
Итак, для оценки инфляции в конце периода по отношению к периоду используются два основных показателя:
1) темп (уровень) инфляции - относительный прирост среднего уровня цен в рассматриваемом периоде
2) индекс инфляции (индекс изменения цен) – рост среднего уровня цен в рассматриваемом периоде
Взаимосвязь между темпом и индексом инфляции
Возникает вопрос — при какой процентной ставке наращение будет только компенсировать инфляцию? Если речь идет о простых процентах, то минимально допустимая (барьерная) ставка:
Для сложных процентов:
Ставку, превышающую , называют положительной ставкой процента.
Владельцы денег предпринимают различные попытки для компенсации обесценения денег. Наиболее распространенной является корректировка ставки процентов, по которой осуществляется наращение, т.е. увеличение ставки на величину так называемой инфляционной премии, иначе говоря, производится индексация ставки. Итоговую величину можно назвать брутто-ставкой.
Обсудим методы определения брутто-ставки. Если речь идет о полной компенсации инфляции в размере брутто-ставки при начислении простых процентов, то необходимую величину находим из равенства:
где – брутто-ставка
Отсюда брутто-ставка для простых процентов:
Величину брутто-ставки для наращения по сложной ставке процента находим из равенства:
Отсюда брутто-ставка для сложных процентов:
Последнюю формулу называют формулой Фишера. Иногда ее еще записывают в виде:
где i — реальная ставка процента
На практике ставку, скорректированную по темпу инфляции, часто рассчитывают иначе, а именно:
Последняя формула по сравнению с предыдущей содержит один дополнительный член, которым при незначительных величинах и можно пренебречь. Если же они значительны, то ошибка (не пользу владельца денег) станет весьма ощутимой.
Условие задачи
Период начисления 9 месяцев, ожидаемый ежемесячный уровень инфляции 1,3%. Под какую процентную ставку ссудных процентов нужно положить первоначальную сумму, чтобы обеспечить реальную доходность 7% годовых (проценты простые)?
Задали объемную контрольную? Скоро важный зачет/экзамен? Нет времени на выполнение работы или подготовку к зачету/экзамену, но есть деньги? На сайте 100task.ru можно заказать решение задач, контрольных или онлайн-помощь на зачете/экзамене 〉〉
Решение задачи
Найдем величину простой ставки процентов, обеспечивающую реальную доходность:
Откуда:
Индекс инфляции за 9 месяцев:
– срок вклада
Подставляя числовые значения, получаем:
Ответ
r=24.3%
К оглавлению решебника по финансовой математике 〉
100task.ru
Эффект Фишера | Азбука трейдера
Начнём сразу с формулировки гипотезы Фишера (эффекта Фишера), которая гласит, что номинальная процентная ставка зависит от двух величин: от реальной процентной ставки и от темпа инфляции. Зависимость эта имеет следующий вид:
i=r+π, где
i – номинальная процентная ставка;
r – реальная процентная ставка;
π – уровень инфляции в стране.
Данная формула получила своё название по имени американского экономиста Ирвинга Фишера внёсшего значительный вклад в теорию денег.
Таким образом, согласно формуле Фишера, номинальная процентная ставка (являющаяся по своей сути ни чем иным как ценой на кредит) также как и цена на любой потребительский товар или услугу, подлежит коррекции через уровень инфляции.
Формула Фишера позволяет оценить реальную прибыльность инвестиций. Так, например, инвестор, вкладывающий деньги в банк под 12% годовых имеет разный реальный доход при различных значениях уровней инфляции. Если инфляция в течение года будет составлять 6%, то реальный процент полученный инвестором будет:
r=i-π=0.12-0.06=6%
Если же предположить, что уровень инфляции за год достигнет значения в 12%, то эффективность инвестиций при данной номинальной процентной ставке сведётся к нулю:
r=i-π=0.12-0.12=0
Полная формула Фишера
Выше приведена формула в упрощённом её виде. Полный её вариант имеет следующий вид:

Как видите, полная формула отличается от приближенной наличием произведения rπ. Простая математика показывает нам, что при уменьшении значений r и π, их сумма уменьшается не так стремительно как их произведение. Следовательно, при π и r стремящихся к нулю, произведением rπ можно пренебречь.
Смотрите сами, при значениях π и r равных 10% их сумма составит 0,1+0,1=0,2=20%, а их произведение: 0,1х0,1=0,01=10%. А при значениях π и r равных 1%, их сумма будет равна 0,01+0,01=0,02=2%, а произведение всего: 0,01х0,01=0,0001=0,01%. То есть, чем меньше значения π и r, тем более точные результаты даёт приближенная формула Фишера.
www.azbukatreydera.ru
ФОРМУЛА ФИШЕРА. Перевод номинальной ставки в реальную и наоборот. — КиберПедия
В процессе оценки необходимо учитывать, что номинальные и реальные (то есть, включающие и не включающие инфляционный компонент) безрисковые ставки.
Номинальная ставка процента— это рыночная процентная ставка без учета инфляции, отражающая текущую оценку денежных активов.
Реальная ставка процента — это рыночная процентная ставка с учетом инфляции
При пересчете номинальной ставки в реальную и наоборот, целесообразно использовать формулу американского экономиста Фишера, выведенную им еще в 30-е годы:
Rн = Rр + Jинф + Rр * Jинф
Rр = (Rн – Jинф) / (1+ Jинф)
где: Rн — номинальная ставка;
Rр — реальная ставка;
Jинф — годовые темпы прироста инфляции.
Важно отметить, что при использовании номинальных потоков доходов коэффициент капитализации (и ее составные части) должны быть рассчитаны в номинальном выражении, а при реальных потоках доходов — реальном. Для преобразования номинальных потоков доходов в реальные нужно номинальную величину разделить на соответствующий индекс цен, то есть выраженное в процентах отношение уровня цен за тот год, в котором возникнут денежные потоки к уровню цен базового периода.
Например:
Объект недвижимости, сданный на условиях чистой аренды, будет приносить по 1000 долл. ежегодно в течение 2-х лет. Индекс цен в текущем периоде равен 140% и ожидается, что в следующем году он составит 156,7%, а через год 178,5%. Для преобразования номинальных величин в реальные, их необходимо выразить в ценах базисного года. Построим базисный индекс цен для каждого из трех лет. Индексы цен текущего года равны 140/140 = 1, для прогнозного периода: первый год — 156,7/140 = 1,119; второй год — 178,5/140 = 1,275.
Таким образом, реальная величина номинальной 1000 долл., которая будет получена в первом прогнозном году, равна 1000 долл./1,119 = 893,65 долл., во 2-м году (1000 долл./1,275) = 784,31 долл.).
Таким образом, в результате инфляционной корректировки происходит приведение ретроспективной информации, используемой в оценке, к сопоставимому виду, а также учет инфляционного роста цен при составлении прогнозов денежных потоков.
Общая идея – между ожидаемой инфляцией и процентной ставкой (доходностью долгосрочных облигаций) существует долгосрочная связь.
Содержание – повышение ожидаемой инфляции вызывает примерно такое же повышение процентной ставки и наоборот.
Уравнение Фишера – формула для количественной оценки связи между ожидаемой инфляцией и процентной ставкой.
Упрощенное уравнение.
Если номинальная процентная ставка N равна 10, ожидаемая инфляция I равна 6, R – реальная ставка процента, то реальная ставка процента равна 4, поскольку R = N – I или N = R + I.
Точное уравнение.
Реальная процентная ставка будет во столько раз отличаться от номинальной, во сколько раз изменяться цены. 1 + R = (1 + N)/(1 + I). Если раскрыть скобки, то в полученном уравнении значение NI при N и I меньше 10% можно считать стремящимся к нулю. В итоге мы и получим упрощенную формулу.
Расчет по точному уравнению при N равном 10 и I равном 6 даст следующее значение R.
1 + R = (1 + N)/(1 + I), 1 + R = (1 + 0,1)/(1 + 0,06), R = 3,77%.
В упрощенном уравнении мы получили 4 процента. Очевидно что граница применение упрощенного уравнение — значение инфляции и номинальной ставки менее 10%.
Билет 4
1.Связь между уровнем рентабельности и авансированным капиталом. Дисконтированный срок окупаемости проекта (на примере).
Доходность и рентабельность – показатели эффективности деятельности организации.
Рентабельность характеризует отношение (уровень) прибыли к авансированному капиталу или его элементам; источникам средств или их элементам; общей величине текущих расходов или их элементам. Показатели рентабельности отражают сумму прибыли, полученную организацией на каждый рубль капитала, активов, доходов, расходов и т.д.
Авансированный капитал – финансы, вложенные в производство для извлечения прибыли, причем не разовой, а регулярной. На эти средства приобретаются материалы, оборудование, здания и многое другое, что необходимо для производственного процесса. Следовательно, это показатель важен для увеличения рентабельности предприятия. Ведь предприниматель, инвестируя финансы, планирует получить больше прибыли и в значительно короткие сроки.
Рентабельность – показатель, который определяет количество прибыли, полученной с каждой единицы вложенных средств. Если предприятие конкурентоспособно и эффективно функционирует, значит, показатель будет расти.
На процесс роста компании оказывает большое влияние оборот авансированного капитала. Увеличение скорости приводит к сокращению производственного цикла и ускорению получения прибыли.
Увеличение скорости оборота авансированного капитала приводит к сокращению производственного цикла и ускорению получения прибыли.
Чтобы ускорить оборот, необходимо выполнить следующие процессы:
· Закупать сырье только высокого качества.
· Оптимизировать работу логистического отдела.
· Регулярно стимулировать реализацию товара различными способами.
· Внедрять в производство инновации, направленные на сокращение производственного процесса.
Теперь от теории перейдем к практике и посмотрим, как рассчитать рентабельность авансированного капитала.
Как рассчитать рентабельность
Для расчетов применятся следующая формула рентабельности авансированного капитала:
Р ав. к. = (Пр/ав. к.) х 100%, где:
Р ав. к. – рентабельность авансируемого капитала;
Пр – чистая прибыль фирмы;
ав. к. – авансированный капитал.
Данный показатель рассчитывается как для определения общего финансового состояния предприятия, так и для инвестора для создания пакета информации, на основании которой он принимает решение о сотрудничестве.
Дисконтированный период окупаемости (Discounted payback period, DPP) является одним из наиболее распространенных и понятных показателей оценки эффективности инвестиционного проекта.
Дисконтирование, по сути, характеризует изменение покупательной способности денег, то есть их стоимости, с течением времени. На его основе производят сопоставление текущих цен и цен будущих лет.
Рассматривая механизм формирования показателя периода окупаемости, следует обратить внимание на ряд его особенностей, снижающих потенциал его использования в системе оценки эффективности инвестиционных проектов.
Дисконтированный срок окупаемости инвестиции (Discounted Payback Period, DPP или DPВP) — это момент времени, когда современная ценность доходов, получаемых при реализации проекта, сравняется с объемом инвестиционных затрат.
Для расчета данного показателя используется формула:
Где,
СFt-годовые доходы
-сумма всех инвестиций
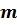 −срок завершения инвестирования
−срок завершения инвестирования
При использовании критерия DPP (и PP) при оценке инвестиционных проектов решения могут приниматься исходя из следующих условий:
— проект принимается, если окупаемость имеет место;
— проект принимается только в том случае, если срок окупаемости не превышает установленного для конкретной компании предельного срока.
Преимущества DPP:
– учет стоимости денег во времени;
— учет факта неравноценности денежных потоков, возникающих в различные моменты времени.
Недостатки DPP::
— в отличие от показателя NPV, он не обладает свойством аддитивности.
— не учитывает последующих притоков денежных средств, а потому может служить неверным критерием привлекательности проекта.
В общем случае определение периода окупаемости носит вспомогательный характер относительно чистой текущей стоимости проекта или внутренней нормы рентабельности.
Коэффициент дисконтирования или барьерная ставка это показатель, используемый для приведения величины денежного потока в n-периоде оценки эффективности инвестиционного проекта, другими словами ставка дисконтирования это процентная ставка, используемая для перерасчета будущих потоков доходов в единую величину текущей стоимости.
Рассматривая механизм формирования показателя периода окупаемости, следует обратить внимание на ряд его особенностей, снижающих потенциал его использования в системе оценки эффективности инвестиционных проектов.
Первой особенностью показателя периода окупаемости является то, что он не учитывает те суммы чистого денежного потока, которые формируются после периода окупаемости инвестиционных затрат:
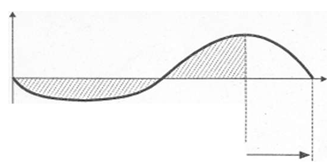
График формирования чистого денежного потока по реальному инвестиционному проекту в течение его полного жизненного цикла
Так, по инвестиционным проектам с длительным сроком эксплуатации после периода их окупаемости может быть получена гораздо большая сумма чистого денежного потока, чем по инвестиционным проектам с коротким сроком эксплуатации (при аналогичном и даже более быстром периоде окупаемости последних).
Второй особенностью показателя периода окупаемости, снижающей его оценочный потенциал, является то, что на его формирование существенно влияет (при прочих равных условиях) период времени между началом проектного цикла и началом фазы эксплуатации проекта. Чем большим является этот период, тем соответственно выше и размер показателя периода окупаемости проекта.
Третьей особенностью периода окупаемости, определяющей механизм его формирования, является значительный диапазон его колебания под влиянием изменения уровня принимаемой дисконтной ставки. Чем выше уровень дисконтной ставки, принятый в расчете настоящей стоимости исходных показателей периода окупаемости. тем в большей степени возрастает его значение и наоборот. Он может быть использован как один из вспомогательных показателей на стадии отбора инвестиционных проектов в инвестиционную программу предприятия (в этом случае инвестиционные проекты с более высоким периодом окупаемости при равенстве других показателей оценки будут предприятием отвергаться).
Дисконтированный срок окупаемости разумно понимать как тот срок, в расчете на который вложение средств в рассматриваемый проект даст ту же сумму денежных потоков, приведенных по фактору времени (дисконтированных) к настоящему моменту, которую за этот же срок можно было бы получить с альтернативного доступного для покупки инвестиционного актива.
Для инвестиционного планирования и выбора антикризисных инвестиционных проектов показатель дисконтированного срока окупаемости проекта практически важен в первую очередь тем, что он указывает на тот горизонт времени в бизнес-плане инвестиционного проекта, в пределах которого план-прогноз денежных потоков по проекту должен быть особенно надежным.
cyberpedia.su
Примеры решения задач по теме 14_2012
Примеры решения задач по теме
«Рынок капитала»
Номинальная ставка процента составляет 10 %, а реальная равна 4 %. Определите ожидаемый темп инфляции.
Решение: 10 — 4 = 6 %
Чему равна номинальная ставка процента, если вложение 2 000 евро в банк на 1 год принесет вкладчику 120 евро дохода?
Решение: 120 / 2 000 х 100 % = 6 %
Инвестору предоставляется возможность профинансировать инвестиционный проект продолжительностью три года. Величина требуемых инвестиций 10 млн. долл. Доход в 1 год ожидается в размере 5 млн. долл., во 2 год — 4 млн. долл. и в 3 год — 3 млн. долл. Стоит ли принимать это предложение, если приемлемая ставка дисконтирования составляет 10 %?
Решение:
PV = 5 / (1+0.1)1 + 4 / (1+0.1)2 + 3 / (1+0,1)3 = 4,55 + 3,31 + 2,25 = 10,11 млн. долл.
NPV = PV – С = 10,11 – 10,00 = 0,11 млн. долл.
Проект привлекателен для инвестирования (NPV >0).
Величина необходимых капиталовложений составляет 90 ДЕ. При этом сумма доходов за год равна 100 ДЕ, а сумма издержек составляет 82 ДЕ. Рассчитайте норму прибыли на капитал.
Решение: NК = (100-82)/90 = 0,2
Величина необходимых капиталовложений составляет 1000 ДЕ. При этом сумма доходов за год равна 800 ДЕ, а сумма издержек составляет 700 ДЕ. Норма прибыли на капитал равна…
а. 0,1
б. 0,7
в. 0,3
г. 1,43
Решение: NК = (800-700)/1000 = 0,1
studfile.net